Table of Contents
Úkol 5 - Řešení problému batohu genetickým algoritmem
- CTU Prague, MI-PAA, ZS 2011
- Autor: Tomáš Borovička (borovto1)
Zadání
- Seznamte se se zvolenou pokročilou iterativní metodou na problému batohu.
Popis problému
Genetické algoritmy jsou typem evolučních algoritmů, algoritmů jež jsou inspirovány evolučními procesy v přírodě. Jedná se o iterativní algoritmy, které v každé iteraci zlepšují množinu řešení (populaci) pomocí operací selekce, křížení, nebo mutace. Výhodou těchto algoritmů, je jejich nezávislost na typu problému. Jedinou jejich znalostí je výpočet fitness funkce, která reprezentuje kvalitu řešení (potomka).
Řešení
Pro řešení jsme zvolil Generational metodu genetického algoritmu, tedy metodu, které v každé iteraci generuje novou populaci. Její princip naznačuje následující pseudokód a popis fází algoritmu.
Pseudokód:
- Vygeneruj výchozí náhodnou populaci P(0).
- N-krát opakuj:
- Vytvoř novou práznou populaci P(N).
- Selekce - vyber rodiče z populace P(N-1)
- Křížení - proveď s rodiči operaci křížení
- Mutace - proveď s potomky operaci mutace
- Přidej potomky do nové populace
- Nahraď starou populaci novou populací P(N-1)=P(N)
- Potomek z populace P(N) s nejlepší kondicí je řešením
Fáze algoritmu
Fitness
Fitness, neboli kondice genotypu, určuje kvalitu řešení. V případě problému batohu je to cena věcí v batohu s podmínkou překročení váhy. V případě překročení váhy je kondice nejhorší možná.
Selekce
Pro selekci jsem implementoval metodu náhodného výběru a metodu turnaje. Použil jsem nakonec pouze metodu turnaje.
- Turnajová selekce
- Z populace náhodně vyberu N prvků, kde N se je velikost turnaje.
- Z těchto N prvků vyberu prvek s nejlepší kondicí.
Křížení
Implementoval jsem jednobodové a dvoubodové křížení. Při křižení dvou genomů se 50% pravděpodobností uskuteční jednobodové křížení a s 50% pravděpodobností dvoubodové křížení.
- Jednobodové křížení
- Dvoubodové křížení
Mutace
Každý gen genomu zmutuje s pravděpodobností, jež lze parametricky určit.
Výsledky měření
Platforma a HW konfigurace
Windows Server 2008 EE x64, Intel Core2 Duo E8500@3.16GHz, 8 GB DDR2
Výchozí nastavení
- Velikost populace 50
- Počet iterací 25
- Pravděpodobnost křížení 0.8
- Pravděpodobnost mutace genu 0.05
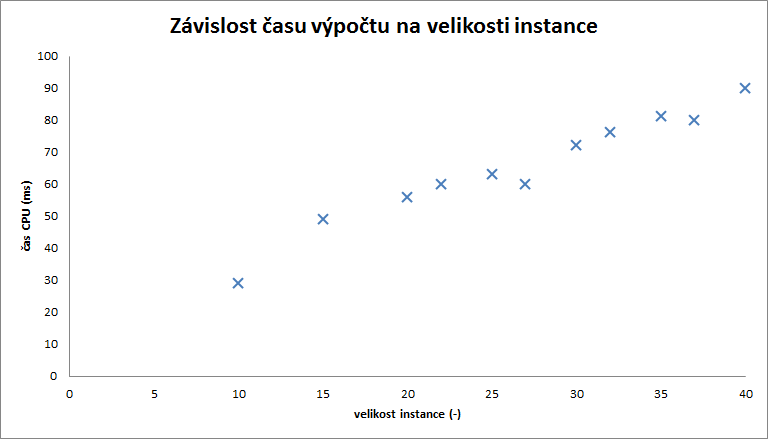
Závislost času na výpočtu na velikosti instance
S velikostí instance roste i výpočetní čas. Podle očekávání výpočetní čas roste s velikostí instance lineárně.
Závislost na počtu iterací
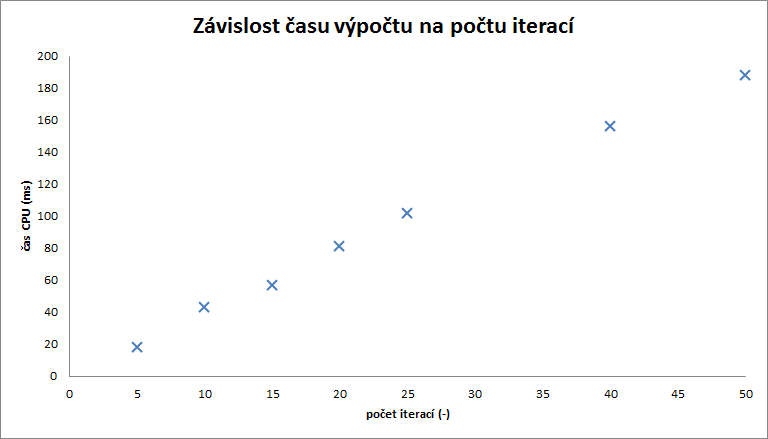
Čas výpočtu
| iterace | 5 | 10 | 15 | 20 | 25 | 40 | 50 |
|---|---|---|---|---|---|---|---|
| cas | 18 | 43 | 57 | 81 | 102 | 156 | 188 |
Podle očekávání čas výpočtu roste lineárně i s počtem iterací.
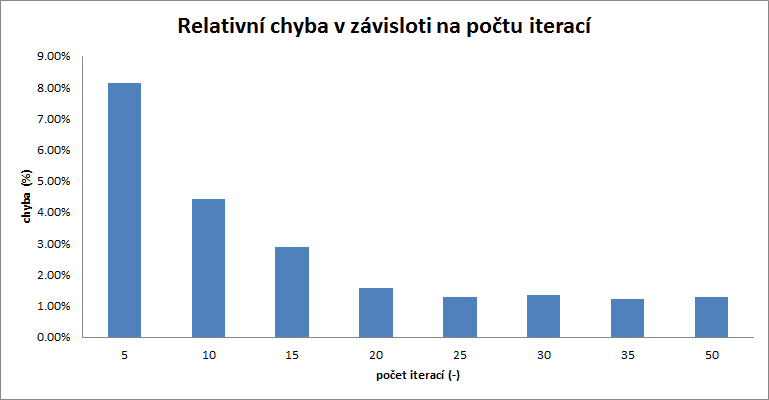
Relativní chyba
| iterace | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 50 |
|---|---|---|---|---|---|---|---|---|
| chyba | 8.14% | 4.42% | 2.88% | 1.56% | 1.29% | 1.35% | 1.22% | 1.28% |
Jak je patrné z grafu, se zvyšujícím se počtem iterací, exponencielně klásá relativní chyba řešení. Po určitém počtu iterací se již řešení nezlepšuje, tento počet iterací je ideální pro výchozí konfiguraci. V tomto případě ustálení nastává po 25 iteracích.
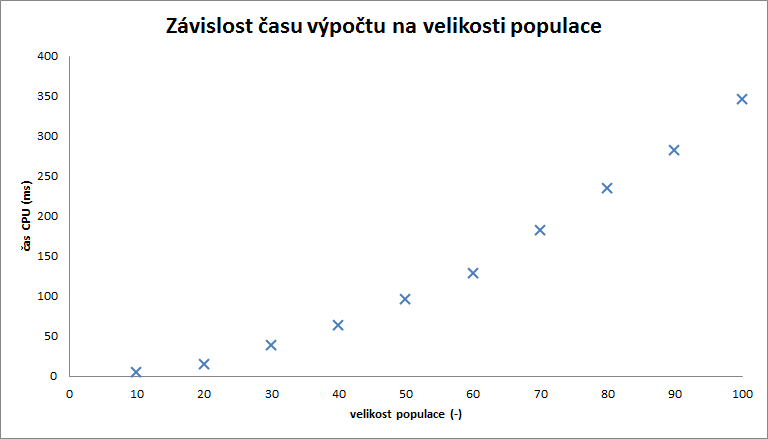
Závislost na velikosti populace
Čas výpočtu
| populace | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| cas | 5 | 15 | 39 | 64 | 96 | 129 | 182 | 234 | 282 | 346 |
Stejně jako u velikosti instance, nebo počtu iterací i s velikostí populace roste čas výpočtu lineárně.
Relativní chyba
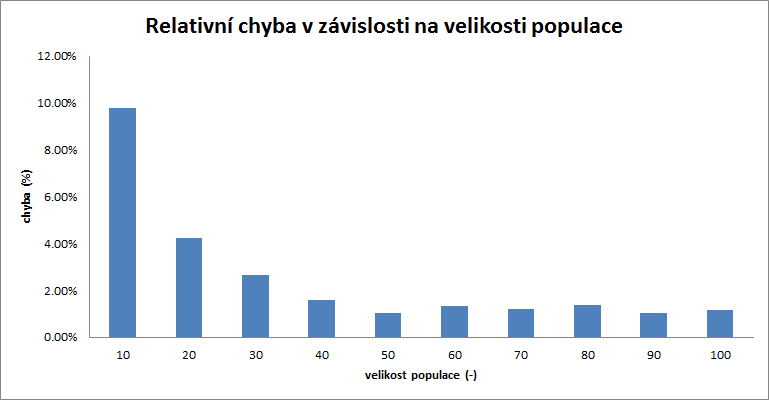
| populace | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| chyba | 9.79% | 4.25% | 2.64% | 1.61% | 1.03% | 1.33% | 1.22% | 1.38% | 1.03% | 1.18% |
Stejně jako s rostoucím počtem iterací, tak i se zvětšující se populací, exponencielně klesá relativní chyba. Ustálení nastalo u populace čítající 50 genomů.
Závislost relativní chyby na pravděpodobnosti mutace
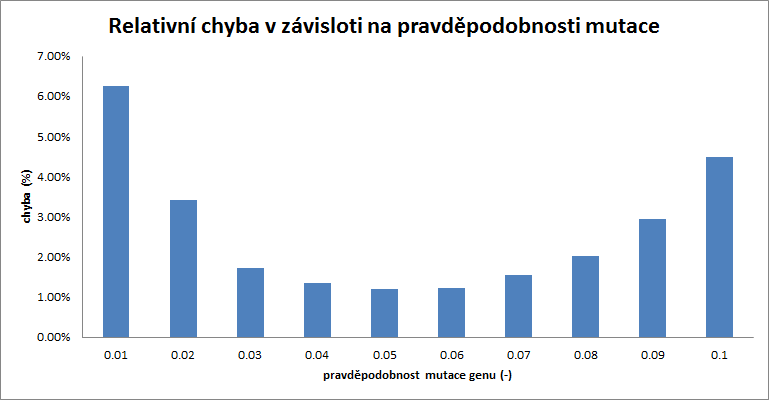
| p | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.1 |
|---|---|---|---|---|---|---|---|---|---|---|
| chyba | 6.26% | 3.43% | 1.72% | 1.35% | 1.20% | 1.24% | 1.54% | 2.03% | 2.95% | 4.48% |
Relativní chyba s nárůstajícím počtem mutací do určité hodnoty klesá, pak ale začne opět výrazně stoupat. Dosažené minimum je ideální pro výchozí nastavení genetického algoritmu pro tento problém.
Závislost relativní chyby na pravděpodobnosti křížení
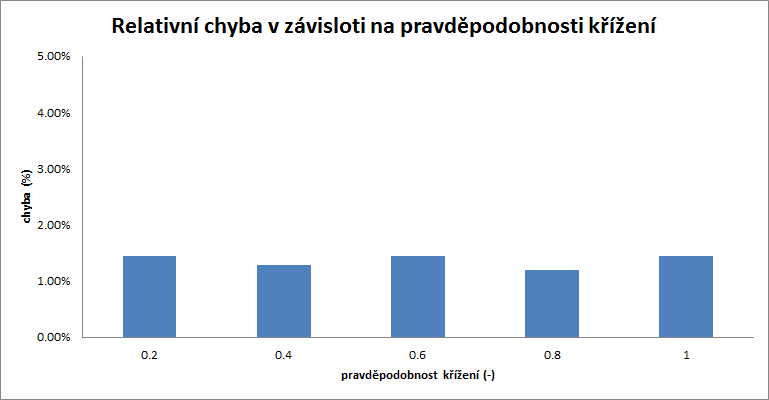
| p | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|
| chyba | 1.45% | 1.28% | 1.44% | 1.20% | 1.45% |
Z grafu není patrná žádná závislost relativní chyby na pravděpodobnosti křížení. Narozdíl od pravděpodobnosti mutace, pravděpodobnost křížení neměla na relativní chybu příliš velký vliv v celém svém rozsahu.
Závěr
Čas výpočtu roste s velikostí instance, velikostí populace a počtem iterací lineárně. Genetický algoritmus lze tedy použít na velké instance s lineárně rostoucími požadavky na výpočetní výkon.
Z experimentu vyplývá, že relativní chyba klesá s počtem iterací do určité hranice, kde se už řešení nezlepšuje. Stejně tak klesá relativní chyba i s velikostí populace až se zastaví a dál zvětšování populace nezlepšuje výsledek. Zajímavé chování vykazuje algoritmus v závislosti na pravděpodobnosti mutace, kdy hodnota relativní chyby klesá do určité hodnoty, kde se zastaví a pak opět roste. Ukazuje se, že je to jeden z parametrů, na který je genetický algoritmus nejvíce citlivý. Naopak pravděpodobnost křížení neměla výrazný vliv na výslednou relativní chybu.
Experimentální nastavení GA s nejlepšími výsledky
- Velikost populace 50
- Počet iterací 25
- Pravděpodobnost křížení 0.8
- Pravděpodobnost mutace genu 0.05
S tímto nastavením dosahoval algoritmus nejmenší relativní chyby a to pod 1,5%, což lze považovat za velmi dobrý výsledek.