Table of Contents
Úkol 3 - problém batohu (knapsack problem)
- CTU Prague, MI-PAA, ZS 2011
- Autor: Tomáš Borovička (borovto1)
Zadání
- Naprogramujte řešení problému batohu:
- metodou větví a hranic (B&B) tak, aby omezujícím faktorem byla hodnota optimalizačního kritéria. Tj. použijte ořezávání shora (překročení kapacity batohu) i zdola (stávající řešení nemůže být lepší než nejlepší dosud nalezené)
- metodou dynamického programování (dekompozice podle vah nebo podle cen)
- modifikujte tento program tak, aby pracoval s omezenou přesností zobrazení vah nebo cen (podle zvoleného přístupu k dynamickému programování) - aproximativní algoritmus.
Popis problému
Je dán batoh s kapacitou W a monožina předmětů N, kde každý předmět má svou váhu w_i a cenu v_i. Úkolem je najít takovou podmonožinu N, která maximalizuje cenu předmětů v batohu a nepřesáhne svou vahou kapacitu batohu W. Problém batohu je kombinatorický optimalizační problém spadající do třídy NP úplných problémů.
Řešení
Řešení metodou větví a hranic (branch & bound)
- Metodaje vychází z původního řešení hrubou silou. Principem metody větví a hranic je ořezávání stavového prostoru o stavy, které nevedou k optimálnímu řešení.
- Ořezávání shora: stav je ukončen, pokud by měla být překročena kapacita batohu.
- Ořezávání zdola: stav je ukončen, pokud je aktuální řešení horššší než nejlepší nalezené.
Část zdrojového kódu - řešení metodou větví a hranic
private Solution SolveBranchAndBound(Solution solution, int idx) { if (idx < 0) return solution; // branch and bound if (_residualValues[idx] + solution.Value <= _bestSolution.Value) return solution; if (solution.ResCapacity < solution.Instance.Items[idx].Weight) return SolveBranchAndBound(solution, idx - 1); var s1 = solution; var s2 = solution.Clone(); // s2.Bits[idx] = true; s2.Value += solution.Instance.Items[idx].Value; s2.ResCapacity -= solution.Instance.Items[idx].Weight; s1 = SolveBranchAndBound(s1, idx - 1); s2 = SolveBranchAndBound(s2, idx - 1); solution = s1.Value > s2.Value ? s1 : s2; _bestSolution = solution; return solution; }
Řešení dynamickým programováním
- Dynamické programování je založeno na dekompozici problémů, řešení jednotlivých subproblému a následné skládání problému s využitím těchto vyřešených subproblémů. Následující algoritmus reší problém dynamickým programováním s dekompozicí podle kapacity. Pro ukládání vesledků využívá algoritmus dvourozměrného pole _solutionCache[kapacita+1, pocet prvku]. Při průchodu pak algoritmus testuje, zda není subproblém vyřešen a pokud ano využije vypočtených hodnot.
Část zdrojového kódu - řešení dynamickým programováním
private Solution SolveDynamic(Solution solution, int idx, int weight) { if (weight < 0) return new Solution(solution.Instance){Value = int.MinValue}; if (idx < 0) return new Solution(solution.Instance); if (_solutionCache[weight, idx] != null) { return _solutionCache[weight, idx].Clone(); } var s1 = solution; var s2 = solution.Clone(); s1 = SolveDynamic(s1, idx - 1,weight); s2 = SolveDynamic(s2, idx - 1,weight-solution.Instance.Items[idx].Weight); s2.Value += solution.Instance.Items[idx].Value; s2.ResCapacity -= solution.Instance.Items[idx].Weight; var result = s1.Value > s2.Value ? s1 : s2; _solutionCache[weight, idx] = result.Clone(); return result; }
FPTAS algoritmus
- FTPAS algoritmus je plně polynomiální časově aproximační algoritmus. Respektive jedná se stále o stejný dynamický algoritmus ovšem využívající plně polynomiální časově aproximační schéma (FPTAS). To umožňuje řešit problém s libovolně stanovenou přesností , kde výpočetní složitost algoritmu se zvyšováním přesnosti neporoste hůře, než polynomiálně.
- Princip algoritmu spočívá v “zaokrouhlení” parametru jež má vliv na počet stavů, které se mohou při řešení vyskytovat. V následujícím algoritmu je tímto parametrem váha předmětů (a s nimi samozřejmě kapacita batohu). Samotné zaokrouhlení spočívá v zanedbání posledních x bitů z váhy předmětu (neboli ve vydělení váhy mocninami 2).
Část zdrojového kódu - FPTAS algoritmus
public void RoundByWeight(int bitsToRound) { Capacity = Capacity >> bitsToRound; foreach (var item in Items) { item.Weight = item.Weight >> bitsToRound; } } public Solution SolveFTPAS(Instance instance) { instance.RoundByWeight(BitsToRound); _solutionCache = new Solution[instance.Capacity + 1, instance.Items.Count]; _solutionCache.Initialize(); return SolveDynamic(new Solution(instance), instance.Count - 1, instance.Capacity); }
Výsledky měření
Platforma a HW konfigurace
Windows Server 2008 EE x64, Intel Core2 Duo E8500@3.16GHz, 8 GB DDR2
Čas výpočtu
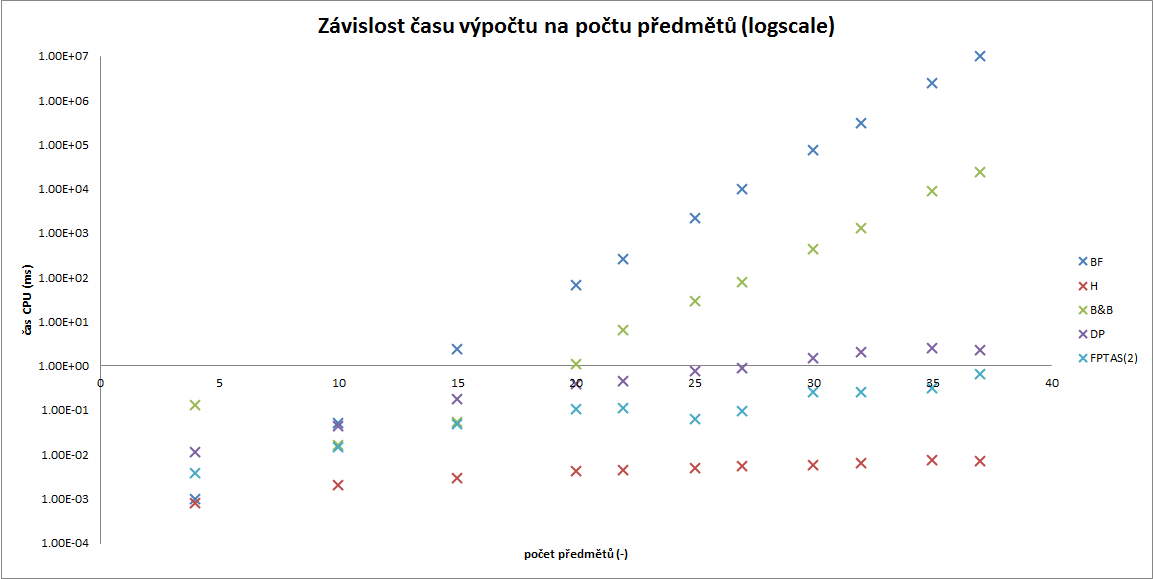
Z tabulky a grafu 1 (v logaritmickém měřítku) je vidět exponenciálně rostoucí čas řešení hrubou silou i metodou branch and bound, i když metodou B&B roste čas výrazně pomaleji. Naopak téměř lineární růst výpočetní času s velikostí instance můžeme pozorovat při dynamickém programování a aproximativním řešení.
| N | BF (ms) | H (ms) | B&B (ms) | DP (ms) | FPTAS(2) (ms) |
|---|---|---|---|---|---|
| 4 | 9.67E-04 | 7.80E-04 | 1.30E-01 | 1.10E-02 | 3.75E-03 |
| 10 | 4.90E-02 | 1.97E-03 | 1.59E-02 | 4.27E-02 | 1.47E-02 |
| 15 | 2.36E+00 | 2.90E-03 | 5.37E-02 | 1.78E-01 | 4.87E-02 |
| 20 | 6.74E+01 | 4.05E-03 | 1.07E+00 | 3.79E-01 | 1.02E-01 |
| 22 | 2.54E+02 | 4.42E-03 | 6.43E+00 | 4.43E-01 | 1.10E-01 |
| 25 | 2.14E+03 | 4.90E-03 | 2.85E+01 | 7.49E-01 | 6.24E-02 |
| 27 | 9.49E+03 | 5.36E-03 | 7.74E+01 | 8.57E-01 | 9.48E-02 |
| 30 | 7.40E+04 | 5.74E-03 | 4.17E+02 | 1.45E+00 | 2.51E-01 |
| 32 | 3.02E+05 | 6.40E-03 | 1.25E+03 | 2.03E+00 | 2.50E-01 |
| 35 | 2.42E+06 | 7.18E-03 | 8.67E+03 | 2.50E+00 | 3.12E-01 |
| 37 | 9.98E+06 | 7.02E-03 | 2.30E+04 | 2.23E+00 | 6.30E-01 |
Závislost chyby a výpočetního času aproximativního algoritmu na zvolené přesnosti zobrazení
Závislost chyby na zvolené přesnosti zobrazení
- Podle očekávání relativní chyba roste s počtem zanedbaných bitů jak ukazuje Graf 2. Výraznější chyba začíná být od tří zaokrouhlených bitů, kde u většiny instancí překračuje hranici 10%.
| 4 | 10 | 15 | 20 | 22 | 25 | 27 | 30 | 32 | 35 | 37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FPTAS 0 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| FPTAS 1 | 0.78% | 1.20% | 0.65% | 1.09% | 1.05% | 1.21% | 0.95% | 1.09% | 0.89% | 0.97% | 0.87% |
| FPTAS 2 | 5.33% | 3.91% | 1.55% | 2.64% | 3.02% | 3.17% | 2.78% | 3.03% | 2.59% | 2.63% | 2.32% |
| FPTAS 3 | 6.09% | 6.60% | 2.65% | 5.46% | 6.82% | 6.31% | 5.46% | 6.15% | 5.80% | 5.53% | 4.90% |
| FPTAS 4 | 18.00% | 13.82% | 5.10% | 9.69% | 12.20% | 11.39% | 10.11% | 11.33% | 10.79% | 10.85% | 9.90% |
| FPTAS 5 | 28.89% | 21.04% | 5.22% | 10.28% | 13.44% | 11.90% | 10.63% | 11.47% | 11.04% | 10.99% | 10.05% |
| FPTAS 6 | 32.70% | 22.75% | 5.22% | 10.28% | 13.48% | 11.90% | 10.63% | 11.47% | 11.04% | 10.99% | 10.05% |
Závislost výpočetního času na zvolené přesnosti zobrazení
- Zanedbáním x nejméně významných bytů redukujeme počet možných stavů problému, důsledkem čehož musí klesat i výpočetní čas. Důkazem je Graf 3, kde FTPAS 0 je vlastně dynamický algoritmus a FTPAS 6 je řešení se zanedbáním 6 posledních bitů.
| 4 | 10 | 15 | 20 | 22 | 25 | 27 | 30 | 32 | 35 | 37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FPTAS 0 | 0.001872 | 0.043992 | 0.181897 | 0.391563 | 0.468315 | 0.904806 | 0.717605 | 1.248008 | 2.184014 | 2.184014 | 2.808018 |
| FPTAS 1 | 0.001872 | 0.025272 | 0.092665 | 0.188761 | 0.211537 | 0.280802 | 0.343202 | 0.624004 | 2.184014 | 0.936006 | 2.496016 |
| FPTAS 2 | 0.002184 | 0.013416 | 0.048048 | 0.094225 | 0.111697 | 0.124801 | 0.124801 | 0.343202 | 0.624004 | 0.624004 | 1.248008 |
| FPTAS 3 | 0.000936 | 0.008424 | 0.020592 | 0.047112 | 0.050544 | 0.0312 | 0.0624 | 0.124801 | 0.183145 | 0.312002 | 0.312002 |
| FPTAS 4 | 0.001248 | 0.005616 | 0.00936 | 0.017784 | 0.024024 | 0.0624 | 0.044616 | 0.0312 | 0.078001 | 0.083617 | 0.112633 |
| FPTAS 5 | 0.001248 | 0.002496 | 0.003744 | 0.007176 | 0.009672 | 0.01248 | 0.01716 | 0.021528 | 0.026832 | 0.029016 | 0.037128 |
| FPTAS 6 | 0.000936 | 0.00156 | 0.002496 | 0.002184 | 0.00312 | 0.00312 | 0.004992 | 0.006552 | 0.004992 | 0.00468 | 0.005304 |
Závěr
Jako nejlepší řešení problému batohu se ukázalo řešení dynamickým programováním, pokud bychom si mohli dovolit ztrátu přesnosti, může nám výrazně snížit výpočetní čas aproximativní řešení s využitím FPTAS.