Table of Contents
Úkol 1 - problém batohu (knapsack problem)
- CTU Prague, MI-PAA, ZS 2011
- Autor: Tomáš Borovička (borovto1)
Zadání
- Naprogramujte řešení problému batohu hrubou silou. Na zkušebních datech pozorujte závislost výpočetního času na n.
- Naprogramujte řešení problému batohu heuristikou podle poměru hmotnost/cena. Pozorujte:
- závislost výpočetního času na n. Grafy jsou vítány (i pro exaktní metodu).
- průměrnou a maximální *relativní chybu* (tj. zhoršení proti exaktní metodě)
Popis problému
Je dán batoh s kapacitou W a monožina předmětů N, kde každý předmět má svou váhu w_i a cenu v_i. Úkolem je najít takovou podmonožinu N, která maximalizuje cenu předmětů v batohu a nepřesáhne svou vahou kapacitu batohu W. Problém batohu je kombinatorický optimalizační problém spadající do třídy NP úplných problémů.
Řešení
Vytvořil jsem dvě řešení - hrubou silou a řešení s využitím jednoduché heuristiky.
Řešení hrubou silou (brute force)
Při řešení hrubou silou procházíme všechny možná řešení problému a hledáme optimální řešení. Algoritmus rekurzivně generuje všechny možné kombinace věcí, které můžeme vložit do batohu, aniž bychom ho přetížili, a hledá optimální řešení. Složitost tohoto algoritmu je 2^|N|.
Část zdrojového kódu - řešení hrubou silou
public Solution SolveBruteForce(Instance instance, Solution solution, int idx) { if (idx < 0) return solution; if(solution.ResCapacity < instance.Items[idx].Weight) return SolveBruteForce(instance, solution, idx-1); Solution s1 = solution; Solution s2 = solution.Clone(); s2.Value += instance.Items[idx].Value; s2.ResCapacity -= instance.Items[idx].Weight; s1 = SolveBruteForce(instance, s1, idx-1); s2 = SolveBruteForce(instance, s2, idx-1); solution = s1.Value > s2.Value ? s1 : s2; return solution; }
Řešení s využitím jednoduché heuristiky (cená/váha)
Další řešení je s využitím jednoduché heuristiky. Heuristika spočívá v seřazení věcí podle poměru cena/váha. Následně do batohu vkládáme věci s nejvyšším poměrem cena/váha, dokud batoh zcela nezaplníme. Výpočetní složitost je značně redukována na cenu řazení + O(|N|).
Část zdrojového kódu - řešení pomocí heuristiky
public Solution SolveWithHeuristic(Instance instance) { instance.SortItems(new ItemByValueWeightComparer()); var solution = new Solution(instance); for (int idx = solution.Count-1; idx >=0 ; idx--) { if (solution.ResCapacity < instance.Items[idx].Weight) continue; solution.Value += instance.Items[idx].Value; solution.ResCapacity -= instance.Items[idx].Weight; }
Výsledky měření
Platforma a HW konfigurace
Windows Server 2008 EE x64, Intel Core2 Duo E8500@3.16GHz, 8 GB DDR2
Způsob měření
Platforma .NET nabízí několik možností jak měřit čas vykonávání algoritmu:
- DateTime.UtcNow
- velmi rychlé volání,
- špatná rozlišovací schopnost (10 milliseconds),
- Stopwatch
- pomalejší než UtcNow,
- nespolehlivé chování na vícejádrových počítačích, nebo počítačích s pohyblivou frekvencí,
- Process.TotalProcessorTime
- měří pouze procesorový čas,
- pokud problém zpracovává více jader, čas se sčítá,
- výrazně pomalejší volání než u UtcNow.
Nejvýhodnější pro měření výkonnosti algoritmu je bezpochyby měření pomocí Process.TotalProcessorTime, které měří pouze procesorový čas, který nás zajímá. Bohužel i při využití Process.TotalProcessorTime nebyla rozlišovací schopnost pro malé instance a heuristiku dostatečná. Bylo nutné opakovat volání algoritmu ve smyčce a výsledný čas podělit počtem opakování. Ilustrace použití v následujícíh částech zdrojového kódu.
Část zdrojového kódu - měření CPU času
TimeSpan begin = Process.GetCurrentProcess().TotalProcessorTime; ... TimeSpan end = Process.GetCurrentProcess().TotalProcessorTime; Console.WriteLine("Execution time: " + (end - begin).TotalMilliseconds + " ms.");
Část zdrojového kódu - měření CPU času pro malé instance a heuristiku
begin = Process.GetCurrentProcess().TotalProcessorTime; for (int i = 0; i < 100000; i++) { solutionH = solver.SolveWithHeuristic(instance.Value); } end = Process.GetCurrentProcess().TotalProcessorTime;
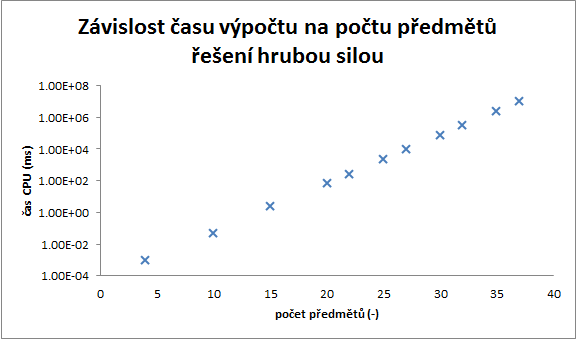
Čas výpočtu
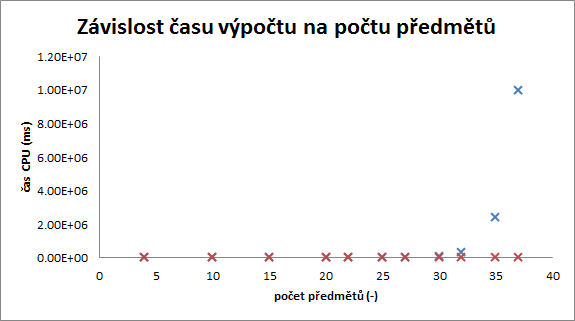
Z tabulky a grafu 1 (v logaritmickém měřítku) je vidět exponenciálně rostoucí čas řešení hrubou silou. Naopak u řešení pomocí heuristiky je vidět lineární nárůst viz graf 2. Obrovský rozdíl ve výpočetním čase nám může přiblížit pohled na graf 3. Problémy s 32,35 a 37 předměty jsem řešil pouze pro dvě instance, jelikož jsou jejich nároky na čas příliš vysoké.
| N | CPU time BF (ms) | CPU time H (ms) |
|---|---|---|
| 4 | 9.67E-04 | 7.80E-04 |
| 10 | 4.90E-02 | 1.97E-03 |
| 15 | 2.36E+00 | 2.90E-03 |
| 20 | 6.74E+01 | 4.05E-03 |
| 22 | 2.54E+02 | 4.42E-03 |
| 25 | 2.14E+03 | 4.90E-03 |
| 27 | 9.49E+03 | 5.36E-03 |
| 30 | 7.40E+04 | 5.74E-03 |
| 32 | 3.02E+05 | 6.40E-03 |
| 35 | 2.42E+06 | 7.18E-03 |
| 37 | 9.98E+06 | 7.02E-03 |
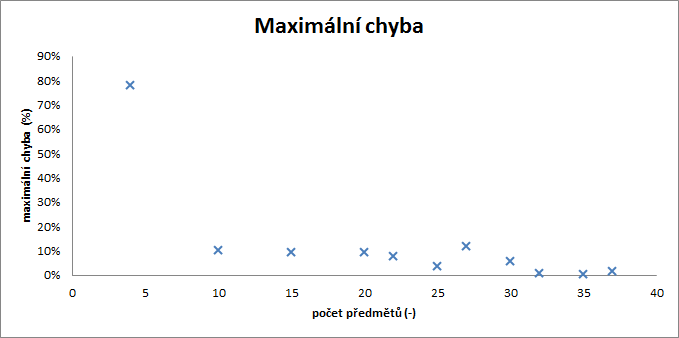
Relativní a maximální chyba
Pro každou instanci jsem spočetl relativní chybu a udělal průměr této chyby přes počet předmětů v instanci a zároveň zaznamenal maximální chybu. Nakonec jsem spočetl celkovou průměrnou relativní odchylku. Data můžeme vidět v tabulce, relativní chybu v grafu 4 a maximální chybu v grafu 5.
| N | ε (%) | ε_max (%) |
|---|---|---|
| 4 | 4.78% | 77.87% |
| 10 | 1.30% | 10.00% |
| 15 | 0.64% | 9.34% |
| 20 | 0.85% | 9.21% |
| 22 | 0.58% | 7.79% |
| 25 | 0.45% | 3.82% |
| 27 | 0.77% | 11.86% |
| 30 | 0.46% | 5.84% |
| 32 | 0.78% | 0.78% |
| 35 | 0.39% | 0.39% |
| 37 | 1.37% | 1.37% |
| avg | 1.12% | - |
Relativní chyba
Relativní chybu spočteme jako ε = ( C(OPT)-C(APX) ) / C(OPT),
- kde C(OPT) je cena optima,
- a C(APX) je cena přibližného řešení.
Relativní chyba se pohybovala do 2%, i když průměrnou hodnotu ovlivnila jedna odlehlá hodnota pro instanci se 4 předměty, byl průměr na 1%, což je velmi dobrý výsledek.
Maximální chyba
Maximální chyba se pohybovala v rozmezí 0-10%, pouze jedna hodnota u instance s 4 předměty byla velmi vysoká a to 78%. To bylo nejspíš způsobeno netestováním vložení do batohu pouze nejdražšího předmětu.
Závěr
Naměřené hodnoty naplnily očekávání a potvrdily, že řešení hrubou silou je pro svou výpočetní složitost u většího počtu předmětů nepoužitelné. Naopak řešení s využitím jednoduché heuristiky dává velmi dobré výsledky (průměrná relativní chyba 1,12%) při výrazně nižší výpočetní složitosti. Pokud je řešen optimalizační problém, je nutné znát cenu optimálního řešení a zhodnotit, zda není výhodnější využít heuristiky s výrazně nižší cenou, avšak s nejistotou nejlepšího optimálního řešení.