Table of Contents
Úkol 6 - Řešení problému splnitelnosti booleovské fromule genetickým algoritmem
- CTU Prague, MI-PAA, ZS 2011
- Autor: Tomáš Borovička (borovto1)
Zadání
Problém řešte některou z pokročilých lokálních heuristik (simulované ochlazování, genetické algoritmy, tabu prohledávání). Volby konkrétních parametrů heuristiky a jejích detailů (operace nad stavovým prostorem, kritérium ukončení, atd. atd.) proveďte sami, tyto volby pokud možno zdůvodněte a ověřte experimentálním vyhodnocením.
Popis problému
Je dána booleovská formule F proměnnných X=(x1, x2, … , xn) v konjunktivní normální formě (tj. součin součtů). Dále jsou dány celočíselné kladné váhy W=(w1, w2, … , wn). Najděte ohodnocení Y=(y1, y2, … , yn) proměnných x1, x2, … , xn tak, aby F(Y)=1 a součet vah proměnných, které jsou ohodnoceny jedničkou, byl maximální.
Obdobný problém, který má optimalizační kritérium ve tvaru „aby počet splněných klausulí byl maximální“ a kde váhy se týkají klausulí, se také nazývá problém vážené splnitelnosti booleovské formule. Tento problém je lehčí a lépe aproximovatelný. Oba problémy se často zaměňují i v seriózní literatuře.
Genetický algoritmus
Genetické algoritmy jsou typem evolučních algoritmů, algoritmů jež jsou inspirovány evolučními procesy v přírodě. Jedná se o iterativní algoritmy, které v každé iteraci zlepšují množinu řešení (populaci) pomocí operací selekce, křížení, nebo mutace. Výhodou těchto algoritmů, je jejich nezávislost na typu problému. Jedinou jejich znalostí je výpočet fitness funkce, která reprezentuje kvalitu řešení (potomka).
Řešení
Algoritmus
Pro řešení byla zvolena Generational metoda genetického algoritmu, tedy metoda, které v každé iteraci generuje novou populaci. Její princip naznačuje následující pseudokód a popis fází algoritmu.
- Vygeneruj výchozí náhodnou populaci P(0).
- N-krát opakuj:
- Vytvoř novou práznou populaci P(N).
- Elitismus - vyber n nejlepší a přidej do nové populace
- Selekce - vyber rodiče z populace P(N-1)
- Křížení - proveď s rodiči operaci křížení
- Mutace - proveď s potomky operaci mutace
- Přidej potomky do nové populace P(N)
- Nahraď starou populaci novou populací P(N-1)=P(N)
- Jedinec z populace P(N) s nejlepší kondicí je řešením
Fáze algoritmu
Počáteční populace
Počáteční populace je generována náhodně pro co nejlepší pokrytí stavového prostoru. Je možné pracovat i s přípustnými řešeními z nějakého SAT solveru. Nicméně to není doporučováno, jelikož stavový prostor by se tím stal značně přetržitým, se špatnou dostupností a heuristika by tak startovala z (možná hlubokého) lokálního minima, navíc možná obklopeného nepřípustnými konfiguracemi.
Fitness
Fitness, neboli kondice genotypu, určuje kvalitu řešení. Jedinci s vyšší kondicí přežívají s větší pravděpodobností. V případě vážené splnitelnosti booleovské formule odpovídá fitness součty váhy konfigurace a penalizace/bonusu za každý nesplněný term respektive za splněnou formuli.
Selekce
Pro selekci byla implementována metoda náhodného výběru a metodu turnaje. V experimentech byla nakonec použita pouze metoda turnaje, kde se dá velikostí turnaje velice dobře řídít selekční tlak.
- Turnajová selekce
- Z populace náhodně vybereme N prvků, kde N se je velikost turnaje.
- Z těchto N prvků vybereme prvek s nejlepší kondicí.
Elitismus
Elitismus umožňuje několika jedincům s nejlepší kondicí přežít do další generace. Tím se zajistí zachování nejlepšího řešení. Je však nutné vybírat dostatečně malou elitní množinu, aby nezačaly generace rychle degenerovat.
Křížení
Křížení představuje výměnu genetické informace mezi dvěma jedinci. Selekcí jsou z populace vybrány dva jedinci - rodiče, kteří se skříží. Jejich potomci obsahují část genetické informace od každého s rodičů.
- Jednobodové křížení - náhodně je zvolen jeden bod (crossover), řetězec od počátku chromozomu ke crossoveru je zkopírován z jednoho rodiče a zbýající část chromozomu od druhého rodiče. Vznikají tak dvanoví potomci.
- Dvoubodové křížení - náhodně jsou zvoleny dva body (crossovery), řetězec od počátku chromozomu k prvnímu crossoveru je zkopírován z jednoho rodiče, část chromozomu od prvního ke druhému crossoveru od druhého rodiče a zbýající část chromozomu od druhého crossoveru opět od prvního rodiče. Taktéž vznikají dva potomci.
- Uniformní křížení - jednotlivé geny jsou náhodně kopírovány z jednoho nebo druhého rodiče.
- Aritmetické křížení - na chromnozomy jsou aplikovány různé aritmetické operace, v tomto případě AND a !XOR.
- Improvement - nejedná se úplně o křížení, algoritmus neguje každý jednotlivý gen chromozomu a testuje zda se zlapšila jeho kondice, pokud ano, vzniká nový genotyp.
- Kombinace výše uvedených
Mutace
Mutace chromozomu zabraňuje při degeneraci populace uváznutí v lokálním minimu. Každý gen genomu s určitou pravděpodobností do další populace zmutuje.
Práce s heuristikou a experimentální vyhodnocení
Platforma a HW konfigurace
Windows Server 2008 EE x64, Intel Core2 Duo E8500@3.16GHz, 8 GB DDR2
Výchozí nastavení GA
- Velikost populace 120
- Počet generací 1000
- Pravděpodobnost křížení 0.95
- Pravděpodobnost mutace genu 0.45
- Velikost turnaje 8
- Elitismus 1
- K = 4
Instance
- Byly použity instance ze SATLIB (http://people.cs.ubc.ca/~hoos/SATLIB/benchm.html.). Tyto instance jsou ve formátu DIMACS, který však neobsahuje váhy proměnných. Vektor vah byl ke každé instanci dogenerován. Do každého souboru instance byl přidán řádek začínající prefixem weights obsahující náhodně vygenerované vah.
- Instancí bylo celkem 50 s 20 proměnnými. Záměrně byli vybrány instance, které je možné řešit hrubou silou v rozumném čase, aby bylo možné provést kontrolu řešení heuristiky. Všechny instance jsou řešitelné.
Relativní chyba
Relativní chybu spočteme jako ε = ( C(OPT)-C(APX) ) / C(OPT),
- kde C(OPT) je cena optima,
- a C(APX) je cena přibližného řešení.
Velikost populace
S větší populací máme větší rozmanitost genotypů a tedy i větší pravděpodobnost nalezení jedince který vede k řešení. Jak bylo dokázáno v 5. úkolu po překonání určité velikosti populace, již další zvětšování nezlepšuje výsledek. Toto tvrzení potvrdil i vývoj relativní chyby a počtu vyřešených insatncí u problému SAT. Hledáme tedy velikost populace, kdy nám již další zvětšování nezlepšuje výsledek.
Jak je vidět na grafu níže, nejlepších výsledků dosahuje algoritmus při velikosti populace 120, kde má najvíce vyřešených instancí s zároveň nízkou relativní chybou.
Pravděpodobnost křížení
Pravděpodobnost křížení určuje, zda ze dvou rodičů vzniknou nový potomci, nebo půjdou rodiče nezměněni do nové generace (případně zmutovaní). Pravděpodobnost křížení značně ovlivňuje rozmanitost populace, při nízkých hodnotách je rozmanitost populace závislá především na mutacích a konvergence ke správnému řešení nastává po větším počtu generací. Naopak při vysoké hodnotě může nastat problém, že se nejlepší nalezené řešení nedostane do nové generace. To je možné řešit dalšími metodami, jako je elitismus.
Nejlepších výsledků dosahuje algoritmus při vysokých hodnotách pravděpodobnosti křížení. V hodnotách 0.9 a 0.95 se kříží těměř všichni jedinci, přesto má algoritmus nejvíce nalezených řešení s relativně malou chybou. To může být díky zachování nejlepších řešení z každé populace, vliv elitismu na algoritmus je probrán později.
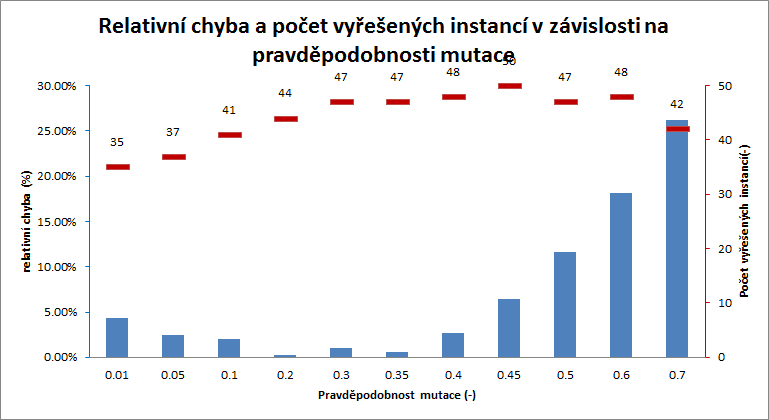
Pravděpodobnost mutace
jak bylo uvedeno, mutace zabraňuje uváznutí řešení v lokalním minimu. Mutace vnáší do populace náhodný šum a napomáhá tak při její degeneraci. Při vysokých hodnotách může mutace způsobit divergenci v populaci, je tedy nutné nejít vhodnou pravděpodobnost mutace genů.
Nejlepších výsledků dosahoval algoritmus pro pravděpodobnost mutace v rozmezí od 0.3 do 0.6. Při vyšších hodnotách řešení přiliš divergovalo, při nízkých naopak rychle uvázlo v lokálních minimech. Jeko nejlepší hodnota vychází pravděpodobnost 0.45, kdy algoritmus vyřešil všechny instance z průměrnou relativní chybou 6.43% a maximální chybou 50%.
Vliv selekčního tlaku (velikosti turnaje)
Selekční tlak je řízen velikostí turnaje, se zvětšující se velikostí turnaje se zvyšuje selekční tlak. Vysoké hodnoty selekčního tlaku vedou k rychlé degeneraci populace a mohou napomoci uváznutí algoritmu v lokálním minimu. Je tedy vhodné najít velikost turnaje k přiměřenému selekčnímu tlaku.
Jako nejlepší pro přiměřený selekční tlak se ukázala velikost turnaje od 6-12 jedinců. Z grafu níže je vidět neschopnost algoritmu řešit (nejspíše) náročnější instance při vysokém selekčním tlaku.
Vliv typu křížení
Pro řešení různých typů problémů se hodí odlišné typy křížení podle toho zda problém je citlivý na zachování stavebních bloků chromozomů (jednobodové, dvoubodové), nebo na jiné operace s geny (uniformní, aritmetické…).
Ukázalo se, že pro SAT problém nedosahuje jadnobodové ani dvoubodové křížení příliš dobrých výsledků a to hlavně se zvyšující se obtížností instancí. Byly tedy implementovány další metody křížení. Ze základních byla první implementována metoda uniformního křížení. Tato metoda vykazuje o něco lepší výsledky, než metody předcházející. Další implementovaná metoda byla metoda aritmetického křížení s využitím funkcí AND a !XOR, ta dosáhla překvapivě dobrých výsledků - snížila relativní chybu a zvýšila počet vyřešených instancí. Nový operátor křížení uvádí ve své práci Evolutionary Computing for the Satisfiability Problem Jin-Kao Hao, toto vylepšení bylo inspirací pro vznik nové metody křížení Improvement. Tato metoda je odlišná od metody, jež popisuje Hao a to hlavně z důvodu, že genetický algoritmus byl navržen tak, aby nevěděl nic o instancích, které řeší, kromě fitness funkce, a bylo cílem tuto vlastnost zachovat. Popis metody Improvement je v části popis řešení. Tato metoda také vykazovala zlepšení oproti metodám základním. Poslední pokus o zlepšení byl zkombinování těchto metod. Při křížení se s 50% pravděpodobností použije metoda Improvement a s 50% pravděpodobností metoda Arithmetic. Kombinování těchto dvou metod, které samostatně vykazovaly lepší vlastnosti než základní metody, se ukázalo jako výhodné - počet splněných instancí se zvýšil a relativní chyba se snížila. Další kombinace metod již nepřinesly zlepšení oproti předchozí, i když jejich výsledky nebyly špatné (v grafu nejsou z důvodu přehlednosti uvedeny). Popsané experimentální výsledky dokazují následující grafy.
Vliv elitismu
Jak již bylo řečeno, elitismus nám zaručuje, že se nám x nejlepších jedineců s populace automaticky dostane do další generace. Tím docíleme toho, že nikdy neztratíme nejlepší řešení. Je však nutné dát pozor na počet těchto jedinců, aby nám nezačala populace rychle degenerovat. Elitismu byl zaveden, jelikož při sledování vývoje populace bylo vidět, že algoritmus už měl řešení blížící se optimu, ale toto řešení se nedostalo do další generace. Pokud byl zvýšen selekční tlak populace zase příliš rychle degenerovala.
Z grafu níže, který zobrazuje výsledky algoritmu bez elitismu, je vidět obrovský vliv elitismu v dané konfiguraci algoritmu. Velká pravděpodobnost křížení a mutace spolu s Generational metodou genetického algoritmu by nemohla fungovat bez elitismu. Pokud bychom nechtěli používat elitismus, museli bychom snížit pravděpodobnost mutace a zvýšit selekční tlak. Další možností je pak druhá metoda genetické algoritmu Steady-State, která nahrazuje vždým nově vzniklým potomkem jedince s aktuálně nejhorší kondicí.
Vývoj populace
Během celého testování byla sledován vývoj populace. Většina vypozorovaných jevů je popsána v ostatních částech práce. Dále bylo vypozorováno, že u nevyřešených obtížných instancí uvízl většinou algoritmus v hlubokém lokálním minimu, ze kterého se nebyl schopen dostat. Pro překonání těchto lokálních extrémů by bylo nutné implementovat sofistikovanější operátory jako například již zmíněný Jin-Kao Hao. Vývoj populace, tak aby mělo jeho příklad nějakou vypovídající hodnotu, je náročné, ne-li nemožné, čitelně zobrazit, proto zde příklad vývoje neuvádím.
Jak kvalita populace roste s počtem generací je vidět na následujícím grafu.
Závislost relativní chyby a počtu splnitelných formulí na obtížnosti formulí K (poměru počtu klauzulí ku počtu proměnných)
Obtížnost instancí se dá řídit (vyjádřit). Jako kritický parametr otížnosti se ukazuje K = počet klauzulí/počet proměnných. U nejtěžších 3SAT problémů je K=4.3. U malých K je mnoho klauzulí, mnoho možných ohodnocení a nalezení řešení je jednoduché. U velkého K je hodně klauzulí ale málo možných kombinací, řešení je tak opět snadno detekovatelné. Úkolem toho měření je ověřit obtížnost testovaných klauzulí pro různá K.
Z grafů níže je jasně patrná zvyšující se obtížnost řešení instancí se zvyšujícím se poměrem počtu klauzulí ku počtu proměnných.
Možnosti zlepšení a neanalyzované parametry
- Zde uvádím další parametry a funkce algoritmu, které by stáli za důkladnější analýzu jejich vlivu na vývoj populace.
- Dále zde uvádím jaké další funkce by bylo možné implementovat.
Větší výchozí populace
Při startu algoritmu je generována větší populace než se kterou pak pracuje algoritmus. Větší počáteční populace dle mého názoru zvyšuje pravděpodobnost nalezení vhodného kandidáta na řešení problému.
Vliv nebyl důkladně otestován.
Výpočet fitness funkce
Výpočet fitness funkce jsme stanovil intuitivně tak, aby byli výrazně upřednostňovány splnitelné konfigurace.
Vliv nebyl důkladně otestován.
Vkládání náhodného vektoru do populace
Do populace vkládám při každé nové generaci jednu novou náhodně vygenerovanou konfiguraci. Chci tím zabránit úplné degeneraci populace.
Vliv nebyl důkladně otestován.
Selekce
V rámci této práce byla implementována pouze jedna metoda selekce (krom náhodné). Určitě by bylo zajímavé implementovat další metody a vzájemně je porovnat.
Závěr
Pro řešení problému vážené splnitelnosti booleovské formule jsem implementoval genetický algoritmus. Algoritmus je navržen maximálně obecně a jedinou jeho znalostí je kondice (fitness) konfigurace.
Výsledky ukazují, že poměr počtu klauzulí ku počtu proměnných je skutečně velmi důležitým ukazatelem obtížnosti při řešení problému splnitelnosti vážené boolovské formule. Jako nejtěžší se ukazují instance s poměrem 4.3 - 4.5, což odpovídá předpokládaným hodnotám.
Při řešení obtížnějších instancí je potřeba zvýšit počet generací i velikost populace, což je intuitivní. Je ale nutné použít sofistikovanějších metod k překonání lokálních extrémů a nalezení řešení blížících, nebo rovnajících se optimu.
Jako výhodné se ukázalo experimentovat s typem křížení, který mohl výrazně zlepšit konvergenci k optimálnímu výsledku. Nejlpším řešením byla kombinace dvou navržených typů křížení.
Během měření bylo vidět, že algoritmus velmi ovlivňuje, kdy najde konfiguraci, která je splnitelná, což může být u náročnějších instancí dosti náhodné. Při nalezení splnitelné formule se dospěl algoritmus k řešení obvykle s relativně malou chybou.
Dala by se udělat řada dalších experimentů a implementovat další metody k vylepšení algoritmu jak je zmíněno v předchozí sekci.
Rozumných výsledků se dá dosáhnout s různými konfiguracemi, jelikož vlivy některých parametrů a funkcí se prolínají. Popsaným experimentálním měřením jsem dospěl k nejlepšímu nastavení genetického algoritmu viz níže.
Nejlepší nastavení GA
- Velikost populace 120
- Počet generací 500
- Pravděpodobnost křížení 0.95
- Pravděpodobnost mutace genu 0.45
- Velikost turnaje 8
- Elitismus 1