Table of Contents
Interaktivní segmentace obrazu s využitím algoritmu pro maximalizaci toku v síti.
- Semestrální projekt: MI-DZO - Digitální zpracování obrazu
- Zpracoval: Tomáš Borovička.
- LS 2011
Úvod
Metoda segmentace obrazu pomocí hledání minimálního řezu, kterou jsem zpracovával, publikovali v roce 2001 Yuri Y.Boykov s Marie-Piere Jolly na “Internation Conference on Computer Vision”.
Plně automatické segmentace nemají díky svým nedokonalým výsledkům tak velké uplatnění jako interaktivní segmentace. Ty jsou velmi populární, hlavně proto, že i malý uživatelský vstup má výrazný vliv na segmentaci a dokáže výsledek výrazně zlepšit.
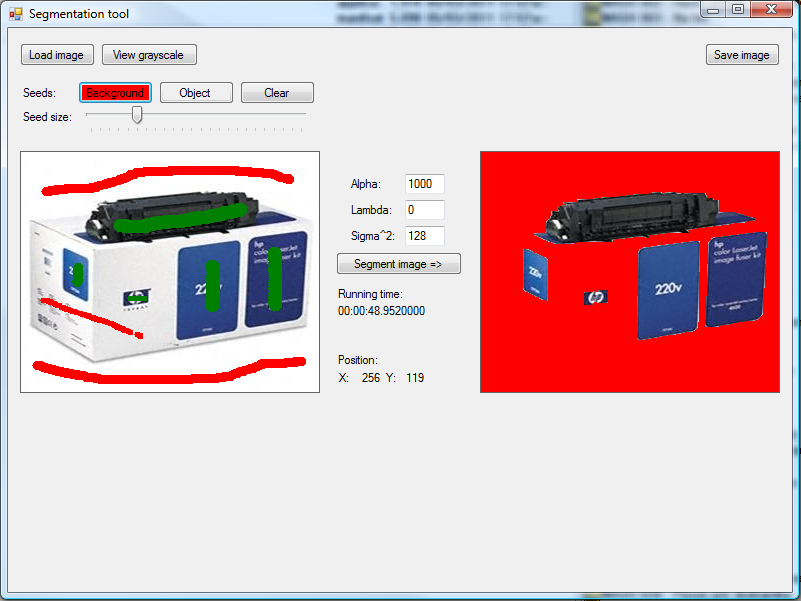
Popisovaná metoda umožňuje rozdělit obraz do dvou segmentů pozadí a objekt. Uživatel označí část pozadí obrázkůjako a část objektu, kteý je pro něho zajímavý. Výsledkem je nalezení optimálního řezu v obrázku, aby byl rozdělen na pozadí a objekt.
Popis
Jak to funguje
Obrázek reprezentujeme jako graf:
- každý pixel odpovídá jednomu uzlu,
- sousedním pixely spojíme hranou (4,8,26 sousedů),
- cena hran mezi uzly odpovídá rozdílu intenzit sousedních pixelů,
- zdrojový uzel (source - S) je spojen s pixely označenými uživatelem jako pozadí hranami nekonečné kapacity,
- cílový uzel (sink - T) je spojen s pixely označenými uživatelem jako objekt hranami nekonečné kapacity.
Sousednost pixelů (4-sousedi)
| x,y-1 | ||||||||||||||||||||||
| x-1, y | x,y | x+1, y | ||||||||||||||||||||
| x,y+1 | ||||||||||||||||||||||
V grafu hledáme maximální tok / minimální řez:
- Ford-Fulkerson algoritmus (Kolmogorov).
Výsledná segmentace:
- Pozadí/objekt je množina uzlů, které jsou dostupné/nedostupné ze zdroje do cíle po nasycení kapacity minimálního řezu.
Cenové funkce
Kapacita hran mezi uzly
- Kapacita C hrany e z uzlu p do uzlu q je stanovena jako:
<m>C_{p,q} = alpha . exp{({ {(I_p - I_q)^2}/{2.sigma^2} })}</m>
- <m>I_p</m> je intezita pixelu p, <m>I_q</m> je intezita pixelu q,
- <m>sigma</m> je konstanta určující strmost exponenciely,
- <m>alpha</m> je konstanta pro normalizaci (škálování) hodnot.
Kapacita hran mezi koncovými uzly a pixely
- Zdroj S
- <m>C_{p,S} = K</m> , <m>p in B</m>
- <m>C_{p,S} = 0</m> , <m>p in O</m>
- Spotřebič T
- <m>C_{p,T} = K</m> , <m>p in O</m>
- <m>C_{p,T} = 0</m> , <m>p in B</m>
Možnost zlepšení segmentace
- Zlepšení spočívá v přidání hran stanovujících míru náležitosti do regionu (pozadí, objekt).
- Zdroj S:
- <m>C_{p,S} = R_p(“Bkg”)</m> , <m>p notin B union O</m>,
- Spotřebič T:
- <m>C_{p,T} = R_p(“Obj”)</m> , <m>p notin B union O</m>,
- kde
- <m>R_p = -ln Pr(I_p|O)</m> respektive <m>R_p = -ln Pr(I_p|B)</m>
Implementace
- Pro implementaci jsem zvolil platformu .net a jazyk C#.
- Pro hledání maximálního toku / minimálního řezu jsem použil Ford-Fulkerson algoritmus.
- Při hledání zlepšující cesty jsem použil BFS.
- Zvolil jsem 4-sousedový systém pro každý pixel.
Algoritmus Ford-Fulkerson (min-cut/max flow) v pseudokódu
set flow 0 on all edges
opt := false
WHILE not opt DO
construct the residual graph G'
find a directed path P from S to T in G' (an augmenting path)
IF exists augmenting path P
THEN update flow f along P
ELSE set opt := true;
set X := the set of vertices in G' reachable from S
END-WHILE
return f as the max flow, and X as the min-cut
END
Ukázka programu
Výsledky
- Obrázky jsou segmentovány s různými nastavením, neexisovalo jedno ideální pro všechny.
- Algoritmus byl pro větší obrázky velmi pomalý, pro obrázek 300×240 pixelů běžel od jedné do tří minut v závislosti na nastavení <m>aplha</m>.
- Obrázky s výraznými přechody a uzavřenými hranami byly segmentovány velice dobře.
- Obrázky, kde byly oblasti s nevýrazným přechodem pozadí-objekt, nebyly segmentovány příliš dobře.
Vybrané výsledky segmentace
Možnost zlepšení
- Kvalita segmentace se dá zlepšit nastavením hran stanovujících míru náležitosti do regionu (pozadí, objekt). Může to být například odvozeno z histogramu uživatelem označených pixelů a vypočtení pravděpodobnosti označení pixelu jako pozadí/objekt.
- Nejvíce prací jako například [2] se zabývá implementací algoritmů pro zrychlením segmentace.
- Další zlepšení mohou využívat vlastností grafů, jež z obrázku vznikají, a redukovat složitost použitých algoritmů. V [4] je uvedeno jak je možné snížit složitost algoritmu pro segmentaci obrázku za využití planarity grafu.
Zdroje
[1] Boykov & Jolly, Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images. ICCV, Vencouver,Canada, July 2001 PDF
[2] Y. Boykov and V. Kolmogorov. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. In 3rd. Intnl. Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition(EMMCVPR). Springer-Verlag, September 2001, to appear.
[3] Daniel Sýkora, Lecture 10:Image Segmentation https://edux.fit.cvut.cz/courses/MI-DZO/
[4] F. R. Schmidt, E. Toeppe, and D. Cremers. Efficient planar graph cuts with applications in computer vision. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR),Miami, Florida, June 2009.