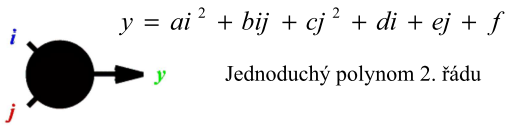Table of Contents
Neuronové sítě
Perceptron
Adaline
- Adaptive Linear Neuron.
- pro vstupy obvykle bipolární aktivace (1 nebo -1),
- výstup nejčastěji bipolární.
Adaptační algoritmus
- Inicializace vah malými náhodnými hodnotami. Přiřazení inicializační hodnoty koeficientu učení α .
- Dokud není splněna podmínka ukončení:
- Pro každý bipolární tréninkový pár s:t (tj. vstupní vektor s a příslušný výstup t)
- Aktivovat vstupní neurony: <m>x_i = s_i</m>.
- Vypočítat skutečnou hodnotu na výstupu:
- <m>y = b + sum{i}{}{x_i w_i}</m>
- Aktualizovat váhové hodnoty a i = 1, …, n:
- <m>w_i(new) = w_i(old) + α(t - y)x_i</m>
- <m>b(new) = b(old) + α (t - y)</m>
- Podmínka ukončení:
- jestliže největší změna váhových hodnot, která se vyskytuje v kroku 2 je menší než maximální povolená chyba, stop
- jinak, pokračovat
Madaline
- Many Adaptive Linear Neurons
- Základním prvkem modelu je neuron Adaline
Backpropagation algoritmus
Fáze algoritmu
- dopředné (feedforward) šíření vstupního signálu tréninkového vzoru,
- zpětné šíření chyby,
- aktualizace váhových hodnot na spojeních.
GMDH MIA
- MIA (Multilayer Iterative Algorithm)
- Patří mezi parametrické sítě
- založen na postupné indukci,
- roste z minimální formy,
- během učení se nastavují její parametry,
- perspektivní neurony (jednotky) přežívají,
- tvorba sítě ukončena, když už přidávání dalších vrstev nezlepšuje přesnost sítě.
- Učí se s učitelem.
- síť vzniká vrstvu po vrstvě,
- při učení se přidávají skryté vrstvy, dokud není splněno kritérium kvality výstupu.
- Jediný typ neuronů.
Neuron GMDH typu MIA
Proces tvorby GMDH MIA
- Máme data v obvyklé formě
- pro každý vektor hodnot vstupních proměnných v1,…,v5 známe výstup y (učení s učitelem).
- Konstruujeme síť s přenosovou funkcí f, která bude modelem systému – pro každý vstupní vektor poskytne výstup blížící se y
- Tvoříme první vrstvu.
- Každý neuron (jednotka) se snaží co nejlépe určit y ze dvou vstupů , ke kterým je připojen.
- Neurony které vygenerujeme nazveme počáte č ní populace.
- Generuje tolik neuronů , kolik je všech možných kombinací dvojic vstupů (pairwise combinations).
- Následuje proces selekce.
- Podle kritéria (viz dále) vybereme neurony, které ve vrstvě zachováme.
- Ostatní neurony zrušíme – umírají. Analogie s genetickými algoritmy, ale zde je jen jedna generace.
- Vybrané neurony ve vrstvě zmrazíme – dále už se nebudou měnit.
- Přidáme další vrstvu.
- Vytvoříme počáteční populaci připojenou k neuron ů m předchozí vrstvy.
- Tyto neurony pro nás vlastně předzpracovávají data ze vstupní vrstvy.
- Každý neuron 2. vrstvy můžeme chápat jako výstup modelu obsahujícího neurony sítě, s nimiž je spojen.
- Opět selekce.
- Každý neuron 2. vrstvy můžeme chápat jako výstup modelu obsahujícího neurony sítě, s nimiž je spojen.
- Tyto modely – stejně složité – spolu bojují o přežití.
- Pokračujeme v přidávání vrstev, dokud je to výhodné (viz dále).
- Optimální model – model y vyhrál v poslední vrstvě.
- Všechny neurony, k nimž není připojen, jsou smazány.