Table of Contents
Úloha 6 - Řešení problému vážené splnitelnosti booleovské formule pokročilou iterativní metodou
- MI-PAA, ZS 2011/12
- Autor: Jaroslav Fibichr (fibicjar)
Zadání
Problém řešte některou z pokročilých lokálních heuristik (simulované ochlazování, genetické algoritmy, tabu prohledávání). Volby konkrétních parametrů heuristiky a jejích detailů (operace nad stavovým prostorem, kritérium ukončení, atd. atd.) proveďte sami, tyto volby pokud možno zdůvodněte a ověřte experimentálním vyhodnocením.
Popis problému
Je dána booleovská formule F proměnnných X=(x1, x2, … , xn) v konjunktivní normální formě (tj. součin součtů). Dále jsou dány celočíselné kladné váhy W=(w1, w2, … , wn). Najděte ohodnocení Y=(y1, y2, … , yn) proměnných x1, x2, … , xn tak, aby F(Y)=1 a součet vah proměnných, které jsou ohodnoceny jedničkou, byl maximální.
Je přípustné se omezit na formule, v nichž má každá klauzule právě 3 literály (problém 3 SAT). Takto omezený problém je stejně těžký, ale možná se lépe programuje a lépe se posuzuje obtížnost instance (viz Selmanova prezentace v odkazech).
Řešení
Pro řešení jsem naimplementoval genetický algoritmus. Princip práce genetického algoritmu je postupná tvorba generací různých řešení daného problému. Při řešení se uchovává tzv. populace, jejíž každý jedinec představuje jedno řešení daného problému. Jak populace probíhá evolucí, řešení se zlepšují.
Následující pseudokód shrnuje princip algoritmu:
1. Vytvoř počáteční populaci P(0) (obvykle náhodnou).
2. Vyhodnoť kvalitu každého jedince v populaci P pomocí ohodnocovací funkce.
3. Vytvoř novou prázdnou populaci P(T).
a. Selekce - použitím operátoru výběru vyber jedince z předchozí populace P(T-1),
b. Křížení - aplikuj na ně operátor křížení a/nebo
c. Mutace - proveď operátor mutace a vytvoř tak nového jedince.
5. Vyhodnoť kvalitu výsledného jedince a vlož jej do nové populace P(T).
6. Nahraď starou populaci P(T-1) novou populací P(T).
7. Opakuj N-krát od bodu 3.
8. Jedinec z poslední populace P(T) s nejvyšší kvalitou je nejlepší nalezené řešení.
Fáze algoritmu
Jednotlivé fáze algoritmu umožňují různé implementace. V následující části popíšu, jak jsem k jednotlivým fázím přistupoval.
Fitness funkce
Fitness funkce ohodnocuje daný genom, určuje jeho kvalitu. Tuto funkci pro problém batohu spočítám jako celkovou cenu věcí v batohu. V případě, že je překročena kapacita batohu, je výsledné ohodnocení rovno 0.
Selekce
Pro selekci rodičů se používám tzv. turnajový výběr (tournament selection):
- z populace náhodně vybereme K jedinců
- z těchto K jedinců vybereme jedince s nejlepší kondicí
Hodnota K je v implementaci ovlivňována parametrem selekční tlak. Tento selekční tlak udává poměr K/n, kde je K je počet vybraných jedinců do turnajového výběru a n je velikost populace.
Křížení
Ke křížení používám jednobodové křížení. To kombinuje genom dvou rodičů tak, že jeden potomek má část genomu od 1. rodiče (od náhodně určeného bodu) a druhou část od 2. rodiče. Druhý potomek těchto rodičů má genomy naopak. Ke křížení dochází jenom s určitou pravděpodobností. Pokud ke křížení nedojde, zůstávají potomci kopiemi rodičů.
Mutace
Naimplementoval jsem jednoduchou mutační funkci. Ta (s určitou pravděpodobností) mění jednotlivé bity genomu. Pro každého jedince a každý bit se uskutečnění mutace určuje zvlášť.
Výsledky měření
Konfigurace HW a OS
- Intel Core2 Duo E7200@2.5GHz, 4 GB DDR2
- Windows 7 64-bit
Výchozí nastavení
Konfigurace parametrů, kterou jsem zvolil (na základě pozorování prováděných během ladění) a ze kterých vycházím při testech je následující:
- Velikost populace = 50
- Počet generací (iterací algoritmu) = 30
- Selekční tlak = 0,3
- Pravděpodobnost křížení = 0,85
- Pravděpodobnost mutace = 0,05
Při testech vždy zafixujeme všechny parametry kromě jednoho, ten měníme a sledujeme výsledky.
Závislost velikosti instance
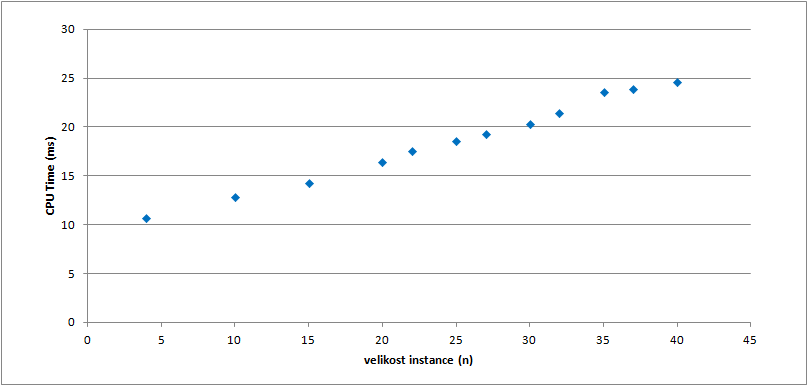
Výpočetní čas
S rostoucím počtem věcí výpočetní čas stoupá. Potvrdilo se očekávání, že čas stoupá s velikostí instance lineárně.
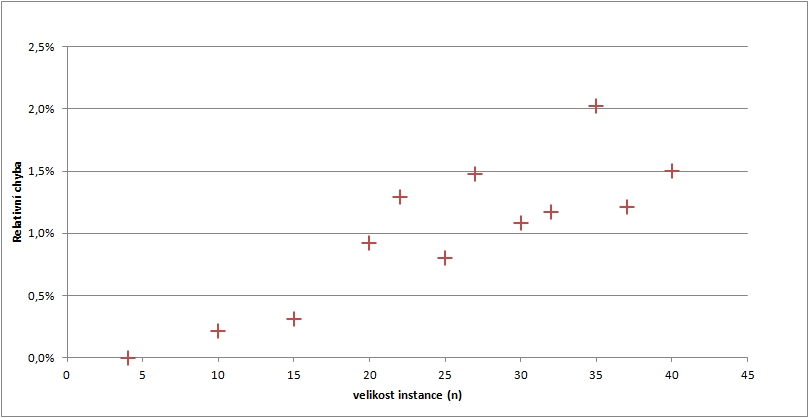
Relativní chyba
Také velikost relativní chyby stoupá s velikostí instance. Tento průběh lze rovněž očekávat, jelikož genetický algoritmus za daných parametrů dojít k dostatečně přesnému řešení. Škálování takového algoritmu by se dalo vyřešit např. zvětšením počtu generací (což zároveň zvýší výpočetní čas, jak je vidět níže).
Závislost na velikosti populace
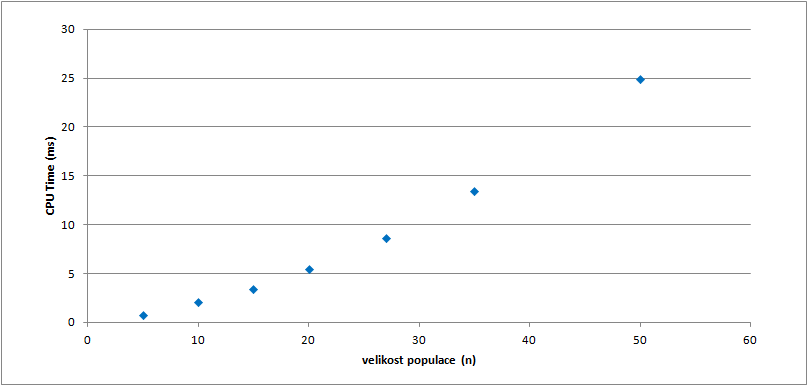
Výpočetní čas
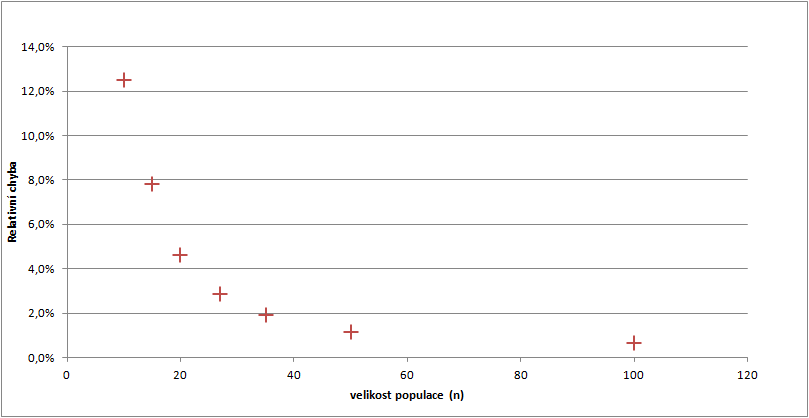
Relativní chyba
Zvyšováním velikosti populace dosahujeme snižování relativní chyby. Chyba klesá exponenciálně, za určitou hranicí už se tedy kvalita zlepšuje pomaleji. Zde například od populace velikosti cca 35 klesá chyba pod 2%.
Závislost na počtu generací
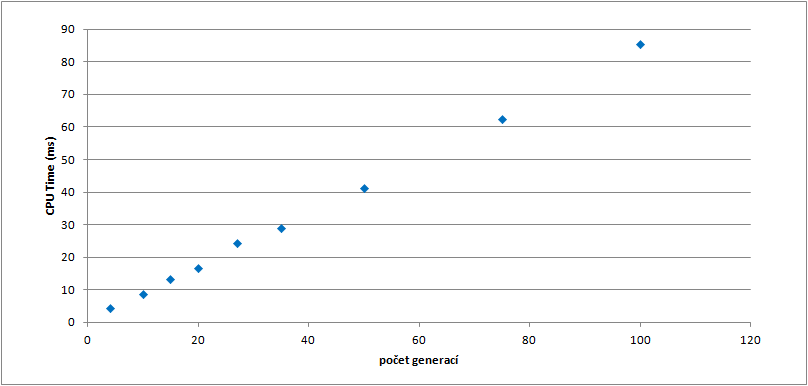
Výpočetní čas
Počet generací ovlivňuje výpočetní čas podobně jako velikost populace nebo počet věcí. Tedy čas roste lineárně.
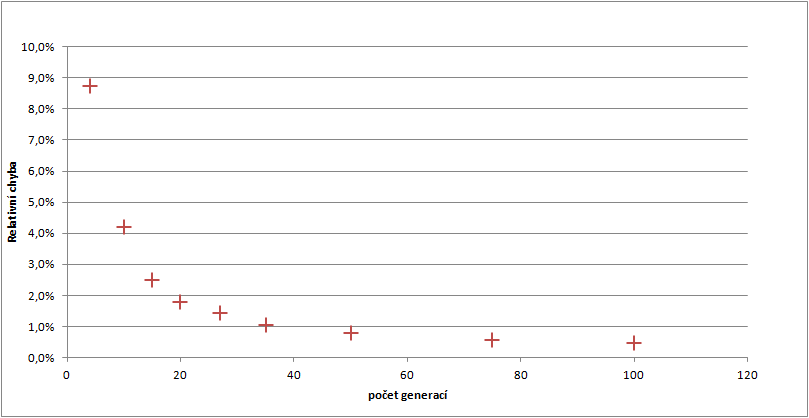
Relativní chyba
I chyba klesá podobně jako u velikosti populace. Pod 2% se dostáváme u hranice 20 generací. Při volbě tohoto parametru je tedy potřeba hledat určitou rovnováhu mezi výpočetním časem a přípustnou chybou výstupu.
Závislost na selekčním tlaku
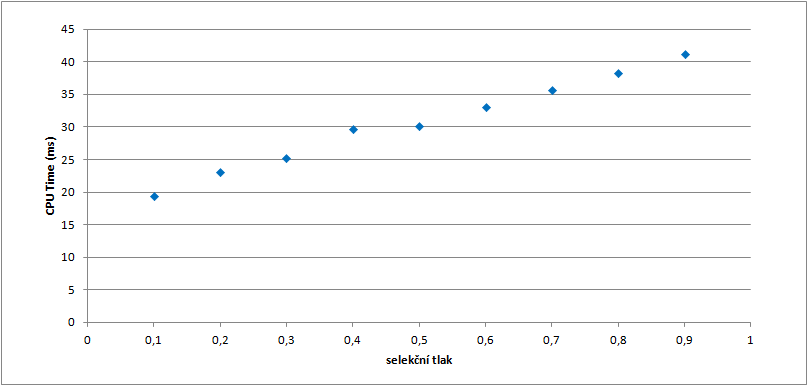
Výpočetní čas
Selekční tlak také ovlivňuje výpočetní čas lineárně. Při zvětšování velikostí turnaje totiž dochází ke zvyšování počtu operací při hledání výherce turnaje, poču křížení i mutací.
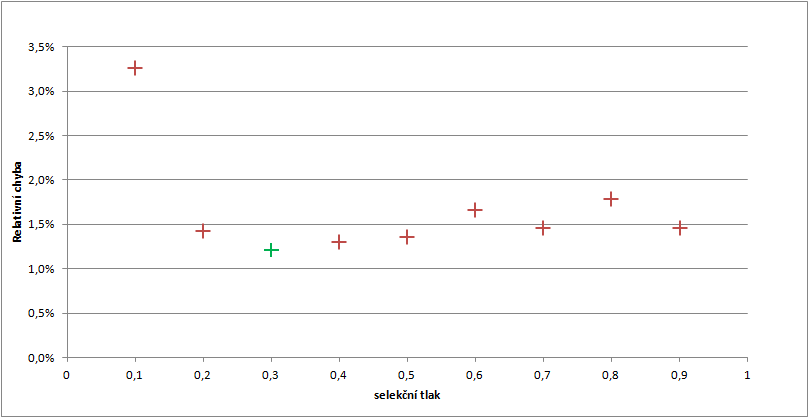
Relativní chyba
Průběh citlivosti na selekční tlak má tvar konvexní křivky s minimem okolo hodnoty 0,3. Prvotní odhad se tedy potvrdil, tato hodnota se zdá pro řešení daného problému optimální.
Závislost na pravděpodobnosti křížení
Pravděpodobnost křížení nemá vliv na čas výpočtu.
Relativní chyba
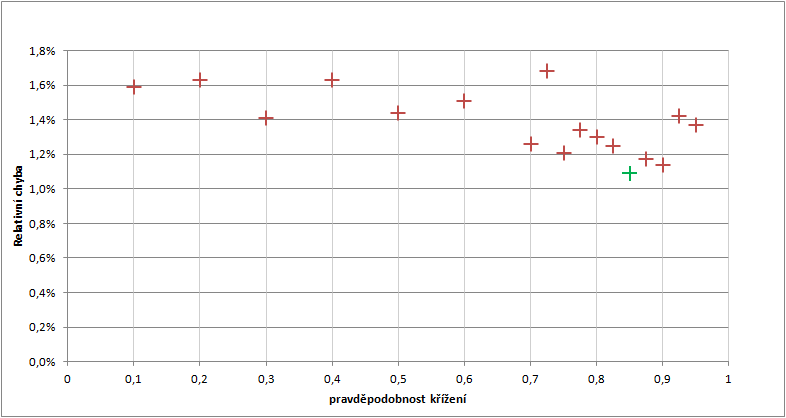
Změna pravděpodobnosti křížení se projevila pouze malou změnou relativní chyby v rozmezí 1-2%. První měření proběhlo na hodnotách pravděpodobnosti po 0,1. Následně jsem dělení zjemnil okolo zdánlivého minima chyby. Ukázalo se, že minimální chybu má algoritmus s nastavením pravděpodobnosti křížení 0,85.
Závislost na pravděpodobnosti mutace
Změna pravděpodobnosti mutace nemá vliv na výpočetní čas.
Relativní chyba
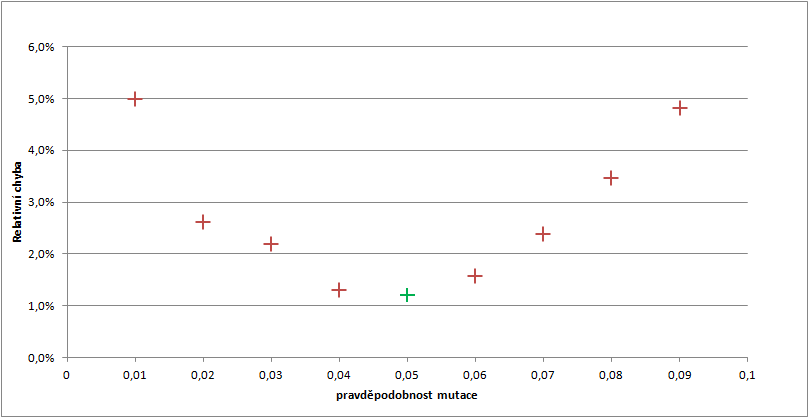
Jako nejvýhodnější se ukázala hodnota 0,05. Křivka v tomto bodě změní jednoznačně své chování z klesání ke stoupání.
Závěr
Navrhnul a naimplementoval jsem verzi genetického algoritmu pro řešení problému batohu. Následně jsem detailním měřením hledal optimální hodnoty pro parametry tohoto algoritmu.
Ukázalo se, že výpočetní čas je lineárně závislý na velikosti instance, velikosti populace i počtu generací. Při hledání optimálního nastavení parametrů je nutno zahrnout do úvah především velikost instance a požadovanou kvalitu výsledku (tedy max. přípustné relativní chyby).
Relativní chyba klesala s velikostí populace i počtem generací. Výrazně ovlivňoval výsledek zvolený selekční tlak i pravděpodobnost mutace. Pravděpodobnost křížení již tak výrazný vliv neměla.
Hodnoty parametrů nejlepší výsledky se téměř shodovaly s výchozím nastavením, tedy:
- Velikost populace = 35
- Počet generací (iterací algoritmu) = 25
- Selekční tlak = 0,3
- Pravděpodobnost křížení = 0,85
- Pravděpodobnost mutace = 0,05
Velikosti instance pro všechna měření byla 40 věcí. Pro vyšší počty by bylo třeba parametry měnit, abychom získaly dostatečně kvalitní řešení (do 2% relativní chyby).