Table of Contents
Úloha 3 - Řešení problému batohu dynamickým programováním, metodou větví a hranic a aproximativním algoritmem
- MI-PAA, ZS 2011/12
- Autor: Jaroslav Fibichr (fibicjar)
Zadání
- Naprogramujte řešení problému batohu:
- metodou větví a hranic (B&B) tak, aby omezujícím faktorem byla hodnota optimalizačního kritéria. Tj. použijte ořezávání shora (překročení kapacity batohu) i zdola (stávající řešení nemůže být lepší než nejlepší dosud nalezené)
- metodou dynamického programování (dekompozice podle vah nebo podle cen)
- modifikujte tento program tak, aby pracoval s omezenou přesností zobrazení vah nebo cen (podle zvoleného přístupu k dynamickému programování) - aproximativní algoritmus.
Popis problému
Řešený problém se shoduje se zadáním v úkolu 1, tedy:
Je dán batoh s kapacitou W a monožina předmětů N, kde každý předmět má svou váhu wi a cenu vi. Úkolem je najít takovou podmonožinu N, která maximalizuje cenu předmětů v batohu a nepřesáhne svou vahou kapacitu batohu W. Problém batohu je kombinatorický optimalizační problém spadající do třídy NP úplných problémů.
Řešení
Naprogramoval jsem řešení zadanéúlohy popsanými metodami. Výsledky měření jsem shrnul do tabulek a grafů a v závěru shrnul nabyté poznatky.
Metoda větví a hranic
Metoda vychází z původního řešení hrubou silou. Úkolem je omezit průchod stavovým prostorem pouze na ty větve, které mají smysl, tedy takové, o kterých můžeme s jistotou říci, že nevedou k optimálnímu řešení. Lze provádět ořezávání dvou typů:
- Shora - do batohu nepřidáváme věci, pokud byla překročena jeho kapacita
- Zdola - do batohu nepřidáváme věci, pokud součet hodnot všech zbývajících věcí, které jsme ještě nezkusili přidat, a dosavadní ceny batohu je menší než doposud nejlepší nalezená celková cena. Tento přístup vyžaduje uchovávání “globální” nejlepší dosažené hodnoty ceny batohu a její případná aktualizace.
Složitost zůstává stejná jako u řešení hrubou silou (O(2n)), metoda by však měla být výrazně rychlejší. Nalezne vždy optimální řešení.
private Solution solveBaB(Instance instance, Solution solution, int index) { if (index < 0) { return solution; } if (instance.items[index].weight > solution.remCapacity) { return solveBaB(instance, solution, index - 1); } if (instance.remValues[index] + solution.value < instance.bestSolution.value) { return solution; } Solution s1 = solution; Solution s2 = solution.clone(); s2.value += instance.items[index].value; s2.remCapacity -= instance.items[index].weight; s2.taken[index] = 1; s1.remValue -= instance.items[index].value; // BaB s2.remValue -= instance.items[index].value; // BaB s1 = solveBaB(instance, s1, index - 1); s2 = solveBaB(instance, s2, index - 1); solution = s1.value < s2.value ? s2 : s1; instance.bestSolution = solution; // BaB return solution; }
Dynamické programování
U dynamického programování dekomponujeme problém na jeho podproblémy. Zvolil jsem variantu dekompozice podle kapacity batohu. Řešení každého vyřešeného podproblému je opět nutné ukládat do “globálního” dvourozměrného pole, které uchovává dosažené hodnoty pro jednotlivé dvojice W (kapacita), i (počet předmětů). V případě, že je podproblém již vyřešen, vezme se tato hodnota z tohoto pole namísto opětovného počítání. Algoritmus se skládá z obou fází - dopřednou i zpětnou. Nepředpočítáváme tedy řešení pro podproblémy, které nejsou pro hledané řešení potřeba.
Složitost tohoto algoritmu je pseudopolynomiální, závisí totiž i na jiném parametru než je počet prvků.
private Solution solveDynamic(Instance instance, Solution solution, int index, int weight) { if (weight < 0) { Solution s = new Solution(instance); s.value = Integer.MIN_VALUE; return s; } if (index < 0) { return new Solution(instance); } // return already known if (instance.solMatrix[index][weight] != null){ return instance.solMatrix[index][weight].clone(); // pomocné pole } Solution s1 = solution; Solution s2 = solution.clone(); s1 = solveDynamic(instance, s1, index - 1, weight ); s2 = solveDynamic(instance, s2, index - 1, weight - instance.items[index].weight); s2.value += instance.items[index].value; s2.remCapacity -= instance.items[index].weight; s2.taken[index] = 1; Solution result = s1.value < s2.value ? s2 : s1; instance.solMatrix[index][weight] = result.clone(); // pomocné pole return result; }
Aproximativní algoritmus (FPTAS)
Aproximativní algoritmus je založen na předchozím dynamickém, tedy na verzi s dekompozicí podle vah. Pomocí FPTAS lze řešit problém se stanovenou přesností a zvyšování přesnosti zvyšuje složitost ne více než polynomiálně. Aproximativní algoritmes se tedy liší se tím, že před samotným spuštěním dynamického algoritmu “zaokrouhlí” kapacitu batohu i jednotlivé hmotnosti vkládaných předmětů. Toho dosáhneme zanedbáním nejnižších bitů těchto hodnot o zvolenou hodnotu.
...
instance.capacity = instance.capacity >> instance.bits;
for (int i = 0; i < instance.itemCount; i++) {
instance.items[i].weight = instance.items[i].weight >> instance.bits;
}
instance.solMatrix = new Solution[instance.itemCount][instance.capacity+1]; // pomocné pole
Algorithm algorithm = new Dynamic();
Solution result = algorithm.run(instance, solution);
return result;
Výsledky měřění
Konfigurace HW a OS
- Intel Core2 Duo E7200@2.5GHz, 4 GB DDR2
- Windows 7 64-bit
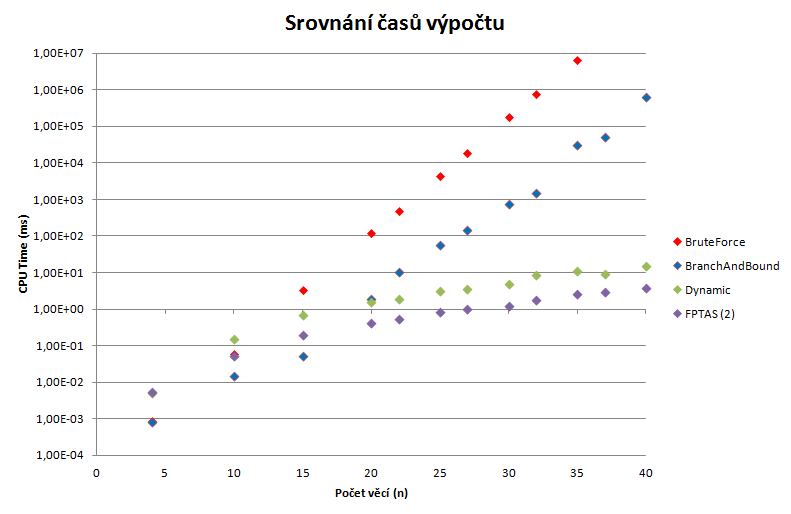
Srovnání výpočetních časů
V následující tabulce a grafu jsou znázorněny výsledky měření jednotlivých algoritmů na daných počtech předmětů a instancí. Je zřetelné, že složitost jednotlivých algoritmů se se zvyšujícím počtem prvků v batohu se je jednoznačně určná uspořádáním:
BruteForce > Branch&Bound > Dynamic > FPTAS(2)
Jediný algoritmus, který nevrací zaručeně optimální řešení je FPTAS, tudíž nejlepší z implementovaných algoritmů, který dává optimální řešení je dynamické programování.
Pozn.: Měření pro velmi krátké časy (< 1 ms) bylo opakováno vícenásobně a následně průměrováno pro dosažení kvalitnějších výsledků.
| n | BruteForce | BranchAndBound | Dynamic | FPTAS (2) |
|---|---|---|---|---|
| 4 | 8,93E-04 | 8,33E-04 | 5,13E-03 | 5,29E-03 |
| 10 | 6,03E-02 | 1,50E-02 | 1,51E-01 | 5,36E-02 |
| 15 | 3,42E+00 | 5,26E-02 | 7,03E-01 | 1,98E-01 |
| 20 | 1,19E+02 | 1,86E+00 | 1,57E+00 | 4,20E-01 |
| 22 | 4,72E+02 | 1,02E+01 | 1,92E+00 | 5,21E-01 |
| 25 | 4,43E+03 | 5,80E+01 | 3,13E+00 | 8,25E-01 |
| 27 | 1,88E+04 | 1,44E+02 | 3,50E+00 | 9,98E-01 |
| 30 | 1,77E+05 | 7,68E+02 | 4,84E+00 | 1,22E+00 |
| 32 | 7,55E+05 | 1,45E+03 | 8,44E+00 | 1,80E+00 |
| 35 | 6,40E+06 | 3,06E+04 | 1,10E+01 | 2,57E+00 |
| 37 | 5,02E+04 | 9,17E+00 | 2,88E+00 | |
| 40 | 6,42E+05 | 1,53E+01 | 3,77E+00 |
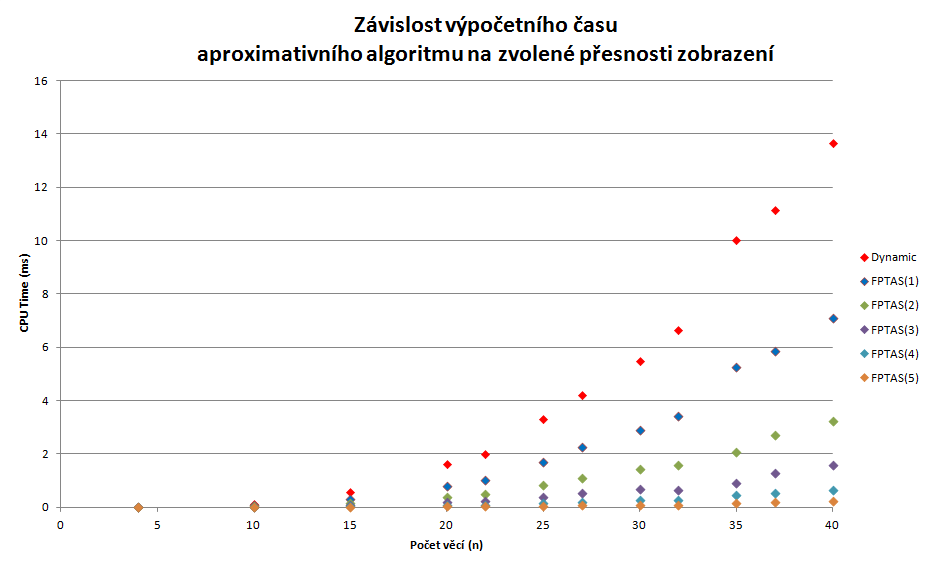
Závislost chyby a výpočetního času aproximativního algoritmu na zvolené přesnosti zobrazení
Podle očekávání se se zvyšujícím počtem zanedbaných bitů:
- snižuje výpočetní čas
- zvyšuje relativní chyba
V tabulce je možné pozorovat výsledky měření pro různé hodnoty zanedbaných bitů. Algoritmus dynamického programování, ze kterého metoda vychází je rovna FPTAS(0). Ta vrací vždy optimální řešení, proto je relativní chyba pro jakýkoliv počet předmětů roven 0. Relativně vysoká míra relativních chyb je z velké části dána nízké “granularitě” vstupních dat. To platí především pro nízká N. V případě zanedbání 3 a více bitů relativní chyba téměř vždy překračuje 5%. Tím například výrazně překračuje chybovost i heuristiky implementované v úkolu č.1.
Z hodnot i grafu naměřených časů lze vyčíst, že čas klesá s počtem zanedbaných bitů exponenciálně. Například pro největší instance se 40 předměty dosáhla v průměru pod 4 ms.
Výpočetní čas (ms)
| n | Dynamic | FPTAS(1) | FPTAS(2) | FPTAS(3) | FPTAS(4) | FPTAS(5) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 5,11E-03 | 6,07E-03 | 5,06E-03 | 4,60E-03 | 4,24E-03 | 3,53E-03 | ||||||
| 10 | 1,19E-01 | 7,44E-02 | 4,01E-02 | 2,29E-02 | 1,42E-02 | 9,93E-03 | ||||||
| 15 | 5,79E-01 | 2,93E-01 | 1,53E-01 | 7,35E-02 | 3,43E-02 | 1,66E-02 | ||||||
| 20 | 1,64E+00 | 8,04E-01 | 3,82E-01 | 1,86E-01 | 8,50E-02 | 3,47E-02 | ||||||
| 22 | 2,00E+00 | 1,03E+00 | 4,87E-01 | 2,33E-01 | 1,00E-01 | 4,12E-02 | ||||||
| 25 | 3,30E+00 | 1,71E+00 | 8,41E-01 | 4,01E-01 | 1,58E-01 | 6,14E-02 | ||||||
| 27 | 4,20E+00 | 2,25E+00 | 1,09E+00 | 5,20E-01 | 2,17E-01 | 7,72E-02 | ||||||
| 30 | 5,48E+00 | 2,90E+00 | 1,43E+00 | 6,88E-01 | 2,92E-01 | 9,89E-02 | ||||||
| 32 | 6,63E+00 | 3,43E+00 | 1,57E+00 | 6,59E-01 | 2,64E-01 | 1,02E-01 | ||||||
| 35 | 1,00E+01 | 5,24E+00 | 2,07E+00 | 8,96E-01 | 4,55E-01 | 1,56E-01 | ||||||
| 37 | 1,11E+01 | 5,87E+00 | 2,72E+00 | 1,31E+00 | 5,54E-01 | 1,84E-01 | ||||||
| 40 | 1,36E+01 | 7,08E+00 | 3,23E+00 | 1,59E+00 | 6,58E-01 | 2,23E-01 | ||||||
Relativní chyba
| n | Dynamic | FPTAS(1) | FPTAS(2) | FPTAS(3) | FPTAS(4) | FPTAS(5) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 0 | 0,78% | 5,33% | 6,09% | 18,00% | 28,89% | ||||||
| 10 | 0 | 1,20% | 3,91% | 6,60% | 13,82% | 21,04% | ||||||
| 15 | 0 | 0,65% | 1,55% | 2,65% | 5,10% | 5,22% | ||||||
| 20 | 0 | 1,09% | 2,64% | 5,46% | 9,69% | 10,28% | ||||||
| 22 | 0 | 1,05% | 3,02% | 6,82% | 12,20% | 13,44% | ||||||
| 25 | 0 | 1,21% | 3,17% | 6,31% | 11,39% | 11,90% | ||||||
| 27 | 0 | 0,95% | 2,78% | 5,46% | 10,11% | 10,63% | ||||||
| 30 | 0 | 1,09% | 3,03% | 6,15% | 11,33% | 11,47% | ||||||
| 32 | 0 | 0,60% | 2,00% | 5,91% | 8,29% | 8,60% | ||||||
| 35 | 0 | 1,16% | 2,77% | 6,60% | 11,30% | 11,30% | ||||||
| 37 | 0 | 0,87% | 2,32% | 4,90% | 9,90% | 10,05% | ||||||
| 40 | 0 | 0,97% | 2,72% | 5,71% | 11,21% | 11,48% | ||||||
Závěr
Naimplementoval jsem podle zadání různé metody řešení zadaného problému batohu. Z měření vyplynulo:
- v případě požadavku na optimálnost řešení je nejvhodnější algoritmus dynamického programování, ten dosahoval nejnižších časů výpočtu
- pokud lze požadavek optimálnosti opustit, lze pomocí algoritmu FPTAS dosahovat ještě výrazně lepších časů, ovšem za cenu snižování přesnosti řešení