Table of Contents
Úloha 2 - Řešení problému přelévání vody
- MI-PAA, ZS 2011/12
- Autor: Jaroslav Fibichr (fibicjar)
Zadání
- Základní problém je definován takto: K dispozici jsou dva kbelíky (předem daných obecně rozdílných objemů), vodovodní kohoutek a kanál. Na počátku jsou oba kbelíky prázdné. Vaším úkolem je docílit toho, aby v jednom kbelíku byla voda o předem stanoveném objemu, přičemž můžete pouze nalít plný kbelík z kohoutku, vylít celý obsah kbelíku do kanálu a přelít jeden kbelík do druhého tak, aby druhý kbelík nepřetekl. Problém lze zobecnit tím, že připustíme užití většího počtu kbelíků, aby na počátku řešení byla v kbelících nějaká voda, a že předepíšeme koncový objem vody v každém kbelíku.
Řešení
Podle zadání jsem navrhnul a implementoval problém přelévání vody. Jednak tedy algoritmem, který řeší problém hrubou silou a za druhé heuristikou.
Řešení hrubou silou
Řešení hrubou silou spočívá v prohledávání stavového prostoru do šířky (BFS).
- Výchozím stavem je stav načtený ze souboru.
- Hledáme takový stav, který odpovídá požadovanému stavu.
Algoritmus expanduje aktualně zpracovávaný stav do všech stavů, které z něho mohou vzniknout. Tyto stavy přidá do kolekce (množiny). Do kolekce není možné vložit dva stejné stavy, tím je zabráněno vytváření cyklů při prohledávání. Pokud algoritmus najde stav, který je shodný s požadovaným stavem, ukončuje výpočet a vrací nalezený stav. Z nalezeného stavu se rekonstruje cesta, kterou vznikl. Prohledáváním do šířky je zajištěno nalezení nejkratší cesty.
Část zdrojového kódu - řešení hrubou silou
// solves the pouring water problem private State solve(Instance instance) { // parameter deteremines the chosen algorithm instance.states = new StateQueue(StateQueue.Method.COMB); instance.states.add(instance.initialState); StateQueue states = instance.states; while (states.getCount() > 0) { State state = states.getFirst(); // solution found if (state.equals(instance.finalState)) { return state; } State newState; // expand State for (int i = 0; i < instance.itemCount; i++) { byte cap = instance.capacities[i]; // fill bucket if ((newState = state.fill(i, cap)) != null) { states.add(newState); } // empty bucket if ((newState = state.empty(i)) != null) { states.add(newState); } // pour bucket to some other for (int j = 0; j < instance.itemCount; j++) { if (j == i) { continue; } if ((newState = state.pour2(i, instance.capacities, j)) != null) { states.add(newState); } } } } // no solution return null; }
Řešení s využitím heuristiky
Při návrhu jsem se snažil nalézt takové pořadí zpracovávání procházených stavů, aby celkový počet navšívených stavů byl co nejmenší. Ostatní charakteristiky průchodu zůstala nezměněna. Jednotlivá řešení se tedy lišila pouze v použité implementaci rozhraní Comparator.
Prioritní zpracování stavů podle počtu správně naplněných kbelíků
Heuristika spočívá v prioritním zpracovávání stavů, které mají nejvíce kbelíků naplněných na požadovaný objem. Tyto stavy mají zřejmě vyšší pravděpodobnost, že budou blíže konečnému stavu, než ostatní. Efekt této heuristiky by se měl zvyšovat s počtem kbelíků.
Část zdrojového kódu - heuristika 1 - Comparator pro správně naplněné kbelíky
public class TotalFinalCmp implements Comparator<State>{ public int compare(State t1, State t2) { int count1 = 0; int count2 = 0; for (int i = 0; i < t1.instance.itemCount; i++) { count1 += (t1.buckets[i] == t1.instance.finalState.buckets[i]) ? 1 : 0; count2 += (t2.buckets[i] == t2.instance.finalState.buckets[i]) ? 1 : 0; } if (count1 < count2) { return 1; } else if (count1 > count2){ return -1; } return 0; } }
Prioritní zpracování stavů podle rozdílu sum objemů kbelíků
Heuristika spočívá v prioritním zpracovávání stavů, které mají nejmenší rozdíl v součtu rozdílů aktuálních objemů kbelíků oproti požadovanému objemu. Tedy pro každý kbelík spočítáme rozdíl objemů: | Vaktuální - Vpožadovaný | a takto spočtené hodnoty sečteme.
Část zdrojového kódu - heuristika 2 - Comparator pro součet rozdílů od požadovaného stavu
public class SumDiffCmp implements Comparator<State>{ public int compare(State t1, State t2) { int sum1 = 0; int sum2 = 0; for (int i = 0; i < t1.instance.itemCount; i++) { sum1 += Math.abs(t1.buckets[i] - t1.instance.finalState.buckets[i]); sum2 += Math.abs(t2.buckets[i] - t2.instance.finalState.buckets[i]); } if (sum1 < sum2) { return -1; } else if (sum1 > sum2){ return 1; } return 0; } }
Kombinace heuristik
Další možností je heuristiky zkombinovat. A to následujícím způsobem - podle heuristiky 2 (SumDiff) spočítám součet rozdílů od požadovaného stavu a od tohoto součtu odečtu konstantu vynásobenou počtem kbelíků, které již mají požadovaný objem. Konstantu volím v závislosti na celkovém objemu kbelíků a jejich počtu. Např. tedy průměrný objem kbelíku vynásobený nějakou konstantou. Tedy porovnávací hodnoty pro jednotlivé stavy byly vypoítány takto:
porovnávaná_hodnota = součet_rozdílů_od_požadovaného_stavu - konst * průměrný_objem_kbelíku * počet_hotových_kbelíků
Lépe je výpočet vidět na kódu Comparatoru:
public class CombCmp implements Comparator<State>{ public int compare(State t1, State t2) { int sum1 = 0; int sum2 = 0; int count1 = 0; int count2 = 0; int value1 = 0; int value2 = 0; for (int i = 0; i < t1.instance.itemCount; i++) { count1 += (t1.buckets[i] == t1.instance.finalState.buckets[i]) ? 1 : 0; count2 += (t2.buckets[i] == t2.instance.finalState.buckets[i]) ? 1 : 0; sum1 += Math.abs(t1.buckets[i] - t1.instance.finalState.buckets[i]); sum2 += Math.abs(t2.buckets[i] - t2.instance.finalState.buckets[i]); } int multiplier = (int) Math.floor(t1.instance.getSumCapacities() / (double)t1.instance.itemCount); value1 = sum1 - (int)Math.floor(1.8 * multiplier * count1); value2 = sum2 - (int)Math.floor(1.8 * multiplier * count2); if (value1 < value2) { return -1; } else if (value1 > value2){ return 1; } return 0; } }
Výsledky měření
- Metrikou měření je počet prošlých stavů, který intuitivněji vyjadřuje kvalitu heuristiky lépe než výpočetní čas.
V tabulce a grafech jsou znázorněny naměřené hodnoty, a to pedevším:
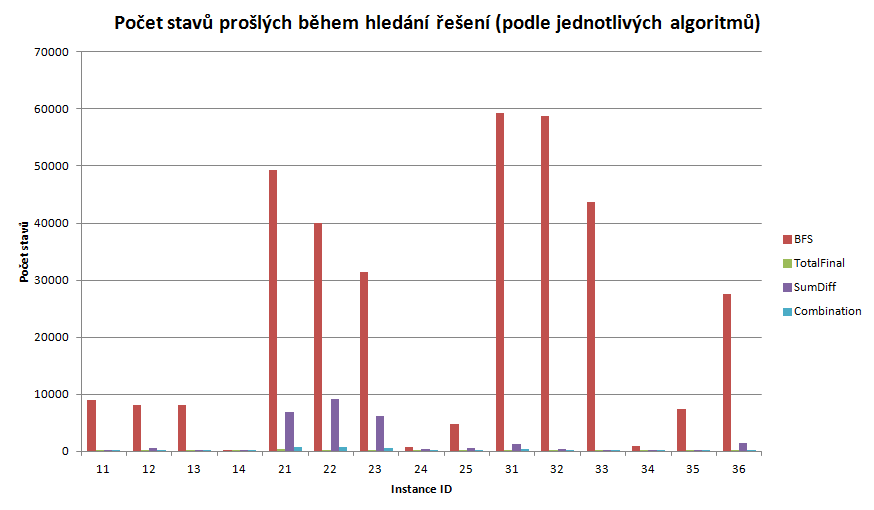
- states - počet prošlých stavů ped nalezením požadovaného řešení
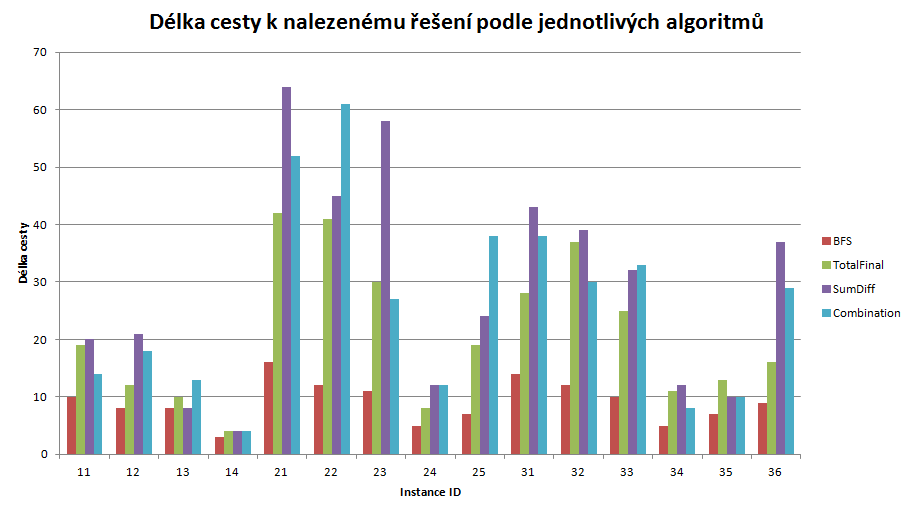
- lpath - délka cesty prošlé ve stavovém prostoru pro nalezené řešení
Výsledné hodnoty z heuristik jsem porovnal s BFS. Pro všechny dané instance i heuristiky jsem spočítal následující hodnoty:
- sBFS/sH - podíl použitých stavů při průchodu stavovým prostorem pomocí BFS a pomocí heuristiky ()
- ε(lpath) - relativní chybu ceny řešení (tedy délku cesty pro nalezené řešení - opět BFS vs. heuristika)
Tyto hodnoty jsem dále zprůměroval (poslední řádek tabulky) přes všechny instance. Z těchto hodnot lze vyčíst, že úspora času (spotřebovaných stavů) byla pro všechny 3 heuristiky enormní, počet prošlých stavů byl roven mezi 1-10% původního BFS řešení. Tato úspora však byla vykoupena poměrně velkými odstupy v délce cesty nalezeného řešení, které bylo o 100-200% delší než u BFS, tedy u nejkratšího možného řešení.
Nejlépe ze všech heuristik vyšla heuristika 1 (TotalFinal). Dosáhla jak nejelpšího výsledku úspory času, tak i nejlepších řešení. Bohužel, kombinování 2 přístupů v heuristice 3 (Combination) se neukázala jako příliš dobrá, ačkoliv v některých instancích heuristiku 1 ve výsledcích předčila.
Tabulka naměřených hodnot
- BFS - Hrubá síla, prohledávání do šířky.
- TotalFinal - Prioritní zpracování stavů podle počtu správně naplněných kbelíků.
- SumDiff - Prioritní zpracování stavů podle součtu objemů kbelíků.
- Combination - Prioritní zpracování stavů podle kombinace dvou předchozích.
- ID - číslo instance
- n - počet kbelíků
- states - počet stavů prošlých během průchodu stavovým prostorem
- lpath - délka cesty (počet stavů) nalezených algoritmem mezi daným počátečním a daným koncovým stavem
- sBFS/sH - poměr počtu prošlých stavů algoritmů BFS a dané heuristiky
- ε(lpath) - relativní chyba ceny nalezeného řešení (tedy délky cesty počátek→konec)
- AVG - průměrná hodnota
| BFS | TotalFinal | SumDiff | Combination | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | n | states | lpath | states | lpath | sBFS/sH | ε(lpath) | states | lpath | sBFS/sH | ε(lpath) | states | lpath | sBFS/sH | ε(lpath) | ||||||||||||||||
| 11 | 5 | 8992 | 10 | 125 | 19 | 1.39% | 90% | 67 | 20 | 0.75% | 100% | 107 | 14 | 1.19% | 40% | ||||||||||||||||
| 12 | 5 | 8055 | 8 | 141 | 12 | 1.75% | 50% | 545 | 21 | 6.77% | 163% | 281 | 18 | 3.49% | 125% | ||||||||||||||||
| 13 | 5 | 8063 | 8 | 27 | 10 | 0.33% | 25% | 12 | 8 | 0.15% | 0% | 18 | 13 | 0.22% | 63% | ||||||||||||||||
| 14 | 5 | 179 | 3 | 6 | 4 | 3.35% | 33% | 6 | 4 | 3.35% | 33% | 5 | 4 | 2.79% | 33% | ||||||||||||||||
| 21 | 5 | 49350 | 16 | 385 | 42 | 0.78% | 163% | 6884 | 64 | 13.95% | 300% | 744 | 52 | 1.51% | 225% | ||||||||||||||||
| 22 | 5 | 40020 | 12 | 170 | 41 | 0.42% | 242% | 9164 | 45 | 22.90% | 275% | 671 | 61 | 1.68% | 408% | ||||||||||||||||
| 23 | 5 | 31387 | 11 | 307 | 30 | 0.98% | 173% | 6176 | 58 | 19.68% | 427% | 550 | 27 | 1.75% | 145% | ||||||||||||||||
| 24 | 5 | 790 | 5 | 15 | 8 | 1.90% | 60% | 449 | 12 | 56.84% | 140% | 55 | 12 | 6.96% | 140% | ||||||||||||||||
| 25 | 5 | 4722 | 7 | 104 | 19 | 2.20% | 171% | 626 | 24 | 13.26% | 243% | 97 | 38 | 2.05% | 443% | ||||||||||||||||
| 31 | 5 | 59199 | 14 | 153 | 28 | 0.26% | 100% | 1368 | 43 | 2.31% | 207% | 337 | 38 | 0.57% | 171% | ||||||||||||||||
| 32 | 5 | 58703 | 12 | 265 | 37 | 0.45% | 208% | 410 | 39 | 0.70% | 225% | 106 | 30 | 0.18% | 150% | ||||||||||||||||
| 33 | 5 | 43770 | 10 | 93 | 25 | 0.21% | 150% | 279 | 32 | 0.64% | 220% | 66 | 33 | 0.15% | 230% | ||||||||||||||||
| 34 | 5 | 1008 | 5 | 32 | 11 | 3.17% | 120% | 52 | 12 | 5.16% | 140% | 23 | 8 | 2.28% | 60% | ||||||||||||||||
| 35 | 5 | 7459 | 7 | 60 | 13 | 0.80% | 86% | 119 | 10 | 1.60% | 43% | 31 | 10 | 0.42% | 43% | ||||||||||||||||
| 36 | 5 | 27532 | 9 | 57 | 16 | 0.21% | 78% | 1415 | 37 | 5.14% | 311% | 144 | 29 | 0.52% | 222% | ||||||||||||||||
| AVG | - | - | - | - | - | 1.21% | 117% | - | - | 10.21% | 188% | - | - | 1.72% | 167% | ||||||||||||||||
Závěr
Experiment ukázal, že využití heuristik může významně snížit počet stavů prošlých ve stavovém prostoru a významně tak zkrátit výpočetní čas. Toto zlepšení je však vykoupeno podstatně horší kvalitou výsledného řešení. To by v případě existenční úlohy (typu najdi nějaké řešení) vůbec nevadilo, v případě optimalizační (najdi co možná nejlepší řešení) už ano. Nejlepších výsledků dosáhla heuristika, která prioritně zpracovávala stavy s co nejvyšším počtem již hotových kbelíků, tedy takových, které již mají požadovaný stav. Druhá navržená heuristika zohledňující co možná nejbližší objem kbelíků požadovanému stavu nebyla tak účinná. Kombinování heuristik také nepřineslo očekávané zlepšení.