Table of Contents
Úkol 2 - problém přelévání vody (water jug problem)
- CTU Prague, MI-PAA, ZS 2011
- Autor: Tomáš Borovička (borovto1)
Zadání
- Základní problém je definován takto: K dispozici jsou dva kbelíky (předem daných obecně rozdílných objemů), vodovodní kohoutek a kanál. Na počátku jsou oba kbelíky prázdné. Vaším úkolem je docílit toho, aby v jednom kbelíku byla voda o předem stanoveném objemu, přičemž můžete pouze nalít plný kbelík z kohoutku, vylít celý obsah kbelíku do kanálu a přelít jeden kbelík do druhého tak, aby druhý kbelík nepřetekl. Problém lze zobecnit tím, že připustíme užití většího počtu kbelíků, aby na počátku řešení byla v kbelících nějaká voda, a že předepíšeme koncový objem vody v každém kbelíku.
Popis problému
Řešení
Vytvořil jsem jedno řešení hrubou silou a několik řešení s využitím heuristiky.
Řešení hrubou silou
Řešení hrubou silou spočívá v prohledávání stavového prostoru do šířky (BFS).
- Výchozím stavem je stav načtený ze souboru.
- Hledáme takový stav, který odpovídá požadovanému stavu.
Algoritmus expanduje aktualně zpracovávaný stav do všech stavů, které z něho mohou vzniknout. Tyto stavy přidá do kolekce (množiny). Do kolekce není možné vložit dva stejné stavy, tím je zabráněno vytváření cyklů při prohledávání. Pokud algoritmus najde stav, který je shodný s požadovaným stavem, ukončuje výpočet a vrací nalezený stav. Z nalezeného stavu se rekonstruje cesta, kterou vznikl. Prohledáváním do šířky je zajištěno nalezení nejkratší cesty.
Část zdrojového kódu - řešení hrubou silou
public ISolution Solve(Instance instance, Methods method) { ... states.Add(new Configuration(instance)); while (states.Count > 0) { var config = states.Get(); // solution found if (instance.IsSolution(config.Volumes)) { return new Solution() {ID = instance.ID, NumOfNodes = states.NumOfStates - states.Count, Steps = config.Step}; } // expand states states.Add(ExpandState(config)); } // solution doesn't exists return null; } public IEnumerable<Configuration> ExpandState(Configuration config) { var result = new LinkedList<Configuration>(); for (int i = 0; i < config.Count; i++) { Configuration newConfig = null; if ((newConfig = Fill(config, i)) != null) result.AddLast(newConfig); if ((newConfig = Empty(config, i)) != null) result.AddLast(newConfig); for (int j = 0; j < config.Count; j++) { if (i == j) continue; if ((newConfig = Pour(config, i, j)) != null) result.AddLast(newConfig); } } return result; }
Řešení s využitím heuristiky
Prioritní zpracování stavů podle počtu správně naplněných kbelíků
Heuristika spočívá v prioritním zpracovávání stavů, které mají nejvíce kbelíků naplněných na požadovaný objem. Heuristika je implementována pomocí Compareru, který je předáván prioritní frontě.
Část zdrojového kódu - řešení pomocí heuristiky
public int Compare(Configuration x, Configuration y) { var valX = RightVolumes(x.Volumes, x.Instance.Finals); var valY = RightVolumes(y.Volumes, y.Instance.Finals); if (valX > valY) return 1; return -1; } private static int RightVolumes(byte[] volumes, byte[] finals) { return volumes.Where((t, i) => t == finals[i]).Count(); }
Prioritní zpracování stavů podle délky ušlé cesty
Heuristika spočívá v prioritním zpracovávání stavů, kterých byo dosaženo nejkratší cestou. Heuristika je implementována pomocí Compareru, který je předáván prioritní frontě.
public class PathLengthComparer : IComparer<Configuration> { public int Compare(Configuration x, Configuration y) { var valX = x.Step; var valY = y.Step; if (valX < valY) return 1; return -1; }
Prioritní zpracování stavů podle rozdílu sum objemů kbelíků
Heuristika spočívá v prioritním zpracovávání stavů, které mají nejmenší rozdíl v sumě objemů kbelíků oproti požadovanému objemu. Heuristika je implementována pomocí Compareru, který je předáván prioritní frontě.
Část zdrojového kódu - řešení pomocí heuristiky
public class SumVolumeComparer : IComparer<Configuration> { public int Compare(Configuration x, Configuration y) { var valX = Sum(x.Volumes, x.Instance.Finals); var valY = Sum(y.Volumes, y.Instance.Finals); if (valX < valY) return 1; return -1; } private static int Sum(byte[] volumes, byte[] finals) { var sumDiff = Math.Abs(volumes.Sum(i => i) - finals.Sum(i => i)); return sumDiff; } }
Kombinování heuristik
Další možností je kombinování heuristik. Zkoušel jsem kombinovat následující heuristiky:
- Prioritní zpracování stavů podle počtu správně naplněných kbelíků + Prioritní zpracování stavů podle délky ušlé cesty
- Prioritní zpracování stavů podle počtu správně naplněných kbelíků + Prioritní zpracování stavů podle rozdílu sum objemů kbelíků
A to následujícím způsobem - pokud mají stavy podle první heuristiky shodnou prioritu, použiji druhou heuristiku.
Výsledky měření
- Metrikou měření je počet prošlých stavů, který intuitivněji vyjadřuje kvalitu heuristiky lépe než výpočetní čas.
Tabulka naměřených hodnot
- BFS - Hrubá síla, prohledávání do šířky.
- Heuristika 1 - Prioritní zpracování stavů podle počtu správně naplněných kbelíků.
- Heuristika 2 - Prioritní zpracování stavů podle délky ušlé cesty.
- Heuristika 3 - Prioritní zpracování stavů podle rozdílu sum objemů kbelíků.
- Heuristika 4 - Prioritní zpracování stavů podle počtu správně naplněných kbelíků + Prioritní zpracování stavů podle délky ušlé cesty.
- Heuristika 5 - Prioritní zpracování stavů podle počtu správně naplněných kbelíků + Prioritní zpracování stavů podle rozdílu sum objemů kbelíků.
| BFS | Huristika 1 | Huristika 2 | Huristika 3 | Huristika 4 | Huristika 5 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | Nodes | Operations | Nodes | Operations | Nodes | Operations | Nodes | Operations | Nodes | Operations | Nodes | Operations |
| 11 | 8992 | 10 | 155 | 22 | 8992 | 10 | 2159 | 12 | 155 | 22 | 155 | 22 |
| 12 | 8055 | 8 | 74 | 12 | 8331 | 8 | 410 | 8 | 74 | 12 | 74 | 12 |
| 13 | 8063 | 8 | 40 | 9 | 8139 | 8 | 91 | 8 | 40 | 9 | 40 | 9 |
| 14 | 179 | 3 | 10 | 3 | 165 | 3 | 13 | 3 | 10 | 3 | 10 | 3 |
| 21 | 49350 | 16 | 525 | 45 | 49344 | 16 | 8264 | 196 | 525 | 45 | 525 | 45 |
| 22 | 40020 | 12 | 169 | 32 | 41962 | 12 | 2248 | 14 | 169 | 32 | 169 | 32 |
| 23 | 31387 | 11 | 334 | 37 | 32481 | 11 | 1483 | 13 | 334 | 37 | 334 | 37 |
| 24 | 790 | 5 | 23 | 6 | 1678 | 5 | 117 | 6 | 23 | 6 | 23 | 6 |
| 25 | 4722 | 7 | 146 | 20 | 4294 | 7 | 420 | 7 | 146 | 20 | 146 | 20 |
| 31 | 59199 | 14 | 423 | 41 | 59199 | 14 | 7748 | 621 | 423 | 41 | 423 | 41 |
| 32 | 58703 | 12 | 176 | 24 | 56961 | 12 | 2369 | 12 | 176 | 24 | 176 | 24 |
| 33 | 43770 | 10 | 59 | 11 | 46503 | 10 | 1770 | 12 | 59 | 11 | 59 | 11 |
| 34 | 1008 | 5 | 13 | 5 | 1010 | 5 | 179 | 6 | 13 | 5 | 13 | 5 |
| 35 | 7459 | 7 | 83 | 9 | 6916 | 7 | 403 | 7 | 83 | 9 | 83 | 9 |
| 36 | 27532 | 9 | 146 | 12 | 26062 | 9 | 1463 | 12 | 146 | 12 | 146 | 12 |
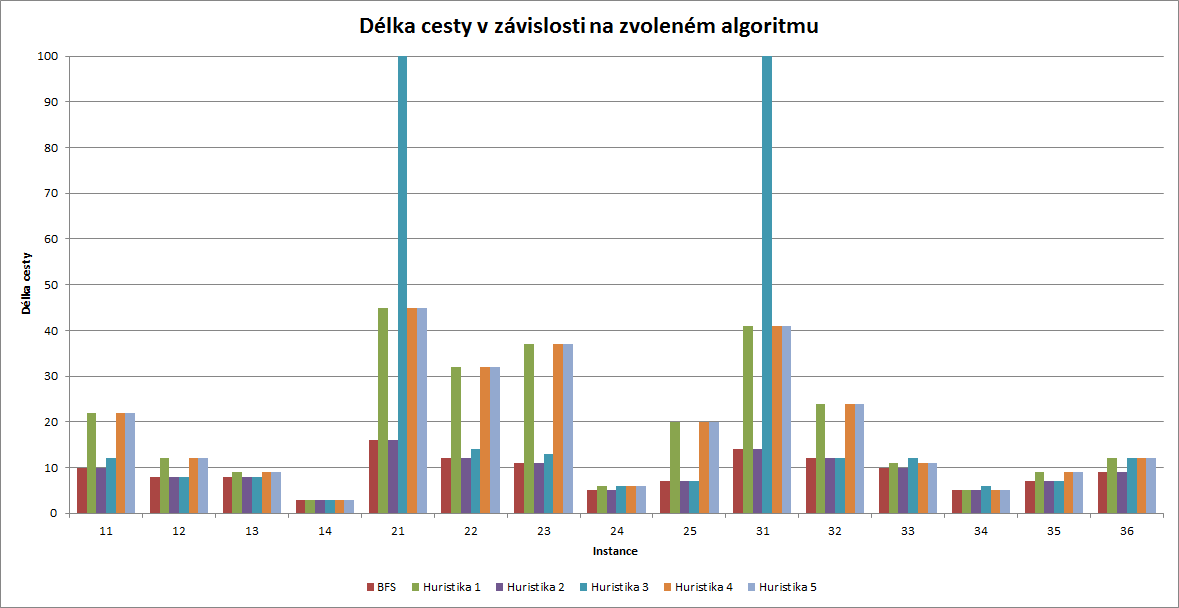
Délka cesty v závislosti na zvoleném algoritmu
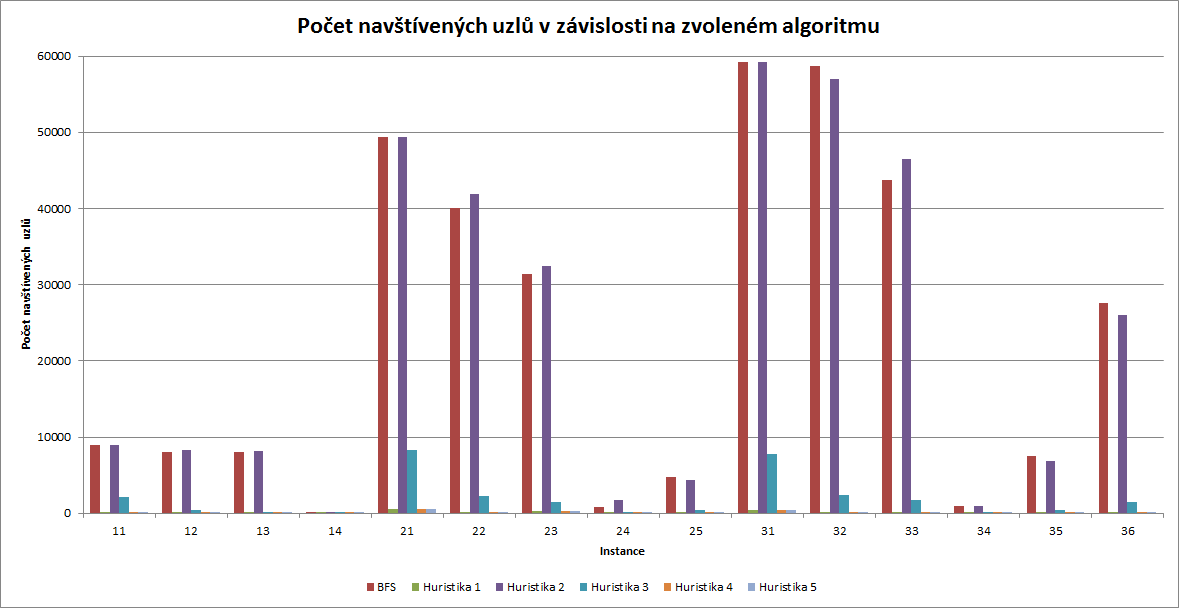
Počet navštívených uzlů v závislosti na zvoleném algoritmu
Závěr
Ukazuje se, že s vzužitím jednoduché heuristiky můžeme značně redukovat počet projítých stavů. Na druhou stranu může heuristika najít výrazně hořší řešení než optimální. Jako nejlepší se ukázala heuristika s prioritním zpracováváním stavů podle počtu správně naplněných kbelíků, které s minimálním počtem prošlých stavů, dosahovalo relativně slušného výsledku. Také heuristika s prioritním zpracování stavů podle rozdílu sum objemů kbelíků měla ve většině instancích dobré výsledky, v několika však měla výsledek velmi špatný. Jako bezvýznamné se ukázalo kombinování výše zmíněných heuristik, jelikož nezlepšilo výsledek.